Hallo,
(a) Das Skizzieren der Funktion und ihrer Grenzen ist im Grunde das wichtigste bei diese Aufgabe Damit allein könnte man das ganze schon lösen.
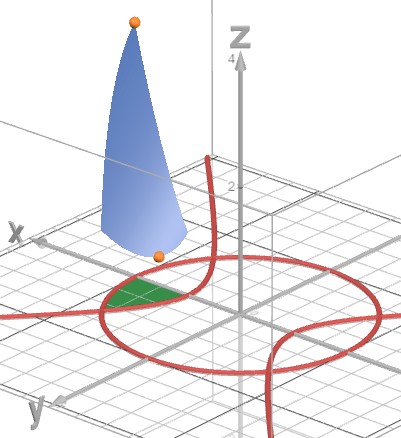
ich habe das hier mit Desmos-3D gemacht. Klicke auf das Bild, dann öffnet sich die zugehörige App. Die ungefähre Lage von Minima und Maxima ist gut zu erkennen. Auf Grund der Einschränkungen bleibt nur der grün markierte Bereich als Definitionsbereich übrig.
Hinweis: Im Optimum ist nur die zweite Nebenbedingung bindend.
Ist ein überflüssiger Hinweis! Ein Blick in die Skizze sollte reichen, dies zu sehen. Das Minimum liegt an der Grenze, die durch die Hyperbel gegeben ist.
(b) "Kuhn-Tucker" hatte ich nie gehört, aber es gibt ja Wikipedia ;-) und das Video vom Mathe-Peter. Wenn es nur darum geht die optimale Lösung zu ermitteln, reicht der Hinweis und Lagrange. Also so:$$f(x,y)=x^2-y \to \min \quad \text{NB.:}\space x^2-y^2 = 1\\ \mathcal{L}(x,y,\lambda) = x^2-y +\lambda(x^2-y^2-1) \\ \nabla \mathcal{L} = \vec{0} \implies \nabla f + \lambda \nabla (x^2-y^2-1) = \vec{0}\\ \begin{aligned} \begin{pmatrix} 2x\\-1 \end{pmatrix} + \lambda\begin{pmatrix} 2x\\-2y \end{pmatrix}&= \vec{0}\\ \implies -4xy &=-2x \\ y &= \frac{1}{2} \lor x = 0\\ \end{aligned}$$Die Lösung \(x=0\) entfällt, da sie die Nebenbedingung in \(\mathbb{R}\) nicht erfüllt. Einsetzen von \(y=1/2\) in die NB gibt dann das Minimum:$$\vec{x}^{*} = \begin{pmatrix} \frac{1}{2}\sqrt{5}\\ \frac{1}{2}\end{pmatrix}$$Nun sollst Du die KTB formulieren und zeigen, dass diese im gefundenen Punkt erfüllt sind. Dazu stelle zunächst die Ungleichungen auf \(g_i(x)\le 0\) um:$$\begin{aligned}g_1:& & x^2+y^2 - 4 &\le 0 \\ g_2: && y^2-x^2 + 1 &\le 0 &&\nabla g_2 = \begin{pmatrix} -2x\\2y\end{pmatrix}\\ g_3: && -x &\le 0 \\ g_4: && -y &\le 0 \end{aligned}$$Nebenbedingungen mit Gleichungen gibt es keine. Folglich reicht es für die 1.KTB, zu zeigen, dass$$\begin{aligned}\nabla f(x^{*}) + \sum\limits_{k=1}^{4} \mu_{k} \nabla g_k(x^{*}) &= \vec{0} \\ \begin{pmatrix} \sqrt{5}\\-1 \end{pmatrix} + \mu_1\begin{pmatrix} \sqrt{5}\\ 1 \end{pmatrix} + \mu_2\begin{pmatrix} -\sqrt{5}\\ 1 \end{pmatrix} + \mu_3\begin{pmatrix} -1\\0 \end{pmatrix} + \mu_4\begin{pmatrix} 0\\-1 \end{pmatrix} &= \vec{0}\end{aligned}$$Und dies ist erfüllt, für \(\mu_{1,3,4} = 0\) und \(\mu_2=1\). Damit ist folgendes erfüllt:$$ g_k(x^{*}) \le 0 \\ \mu_k \ge 0 \\ \mu_k \cdot g_k(x^{*}) = 0 \quad \forall k \quad\text{Bem.:}\space g_2(x^{*})=0$$
(c) an Hand der Graphik ist klar, dass sich das Maximum im Schnittpunkt des Kreises mit der positiven X-Achse befindet:$$x^{*} = \begin{pmatrix} 2\\ 0\end{pmatrix}$$
(d) offensichtlich sind nun \(g_1\) und \(g_4\) die relevanten Grenzen. Da sich das Maximum genau auf dem Schnittpunkt beider Grenzen befindet, gibt es für diesen Fall sicher noch einen Hinweis in Deinem Script.
(e) die grüne Fläche oben im Bild ist konvex. Also sollte das auch in beiden Fällen ein 'konvexes Programm'
sein. Ich bin aber da kein Experte (s.o.)
Gruß Werner