Aufgabe:
…
Hallo, was genau muss man denn noch zeigen, damit man die Konservativität beweist?

Text erkannt:
Seien \( v_{1}, v_{2}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) die Vektorfelde gegeben durch
\( v_{1}(x, y, z)=\left(2 x y+z^{3}, x^{2}, 3 x z^{2}\right), \quad v_{2}(x, y, z)=\left(e^{y}, x e^{y}, 2 z\right) \)
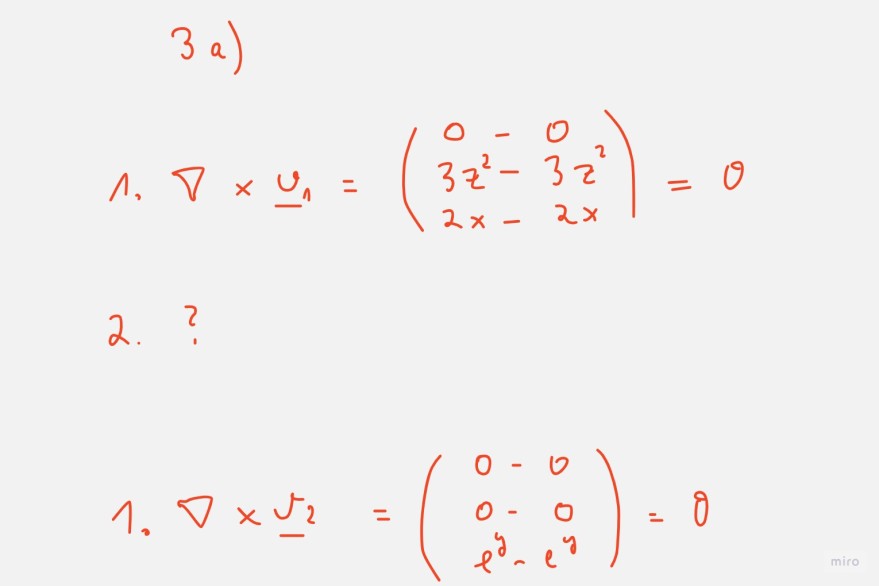
Text erkannt:
\( 3 a) \)
1. \( \nabla \times \underline{u}_{1}=\left(\begin{array}{c}0-0 \\ 3 z^{2}-3 z^{2} \\ 2 x-2 x\end{array}\right)=\theta \)
2. ?
1. \( \nabla \times \underline{v}_{2}=\left(\begin{array}{cc}0-0 \\ 0-0 \\ e^{y}-e^{y}\end{array}\right)=0 \)
Problem/Ansatz: