Für welches t hat die Funktion genau eine Nullstelle?

Question

Aufgabe:

F(x)=x²+tx+16

Problem/Ansatz:

Für welches t hat die Funktion genau eine Nullstelle ? Wie lautet diese Nullstelle? Wie löse ich das? Ich war da nicht da. Danke. Ist das eine quadratische Gleichung wegen x² oder ein Polynom?

Answer 1

Für t=8, denn 0=x²+8x+16=(x+4)² hat nur die Lösung x= - 4.

0=x²+8x+16 ist eine quadratische Gleichung, x²+8x+16 ist ein Polynom.

Answer 2

x²+tx+16 = 0 

<=>  x= -t/2 ± √(t^2/4 - 16)

Genau eine Nullstelle, also bei t^2 / 4 = 16  bzw  t^2 = 64   also t=8 oder t=-8.

Dann ist die Nullstelle -4  bzw 4.

Comments

Danke bin sogar selber auch auf t 8 gekommen weiß aber nicht genau was ihr mit der 4 meint habe gedacht so wird die Wurzel 0 und somit bleibt 8 plus minus stehen, ist der Ansatz richtig?

---

Könnt ihr mir erklären warum es bei der PQ Formel in der Wurzel t/4 sind sehe gerade in den Lösungen dass der Lehrer es so ch mit /4 macht in der Wurzel muss die Wurzel dann so aussehen Wurzel: t/4 - q/4

---

Zwischenschritt:

0=(x+4)² Auf beiden Seiten die Quadratwurzel ziehen:

0=x+4     |-4

-4=x

---

Also meine generell wenn man ausklammert und dann die PQ anwendet benutzt er jetzt in der PQ: -x/2 in der Wurzel dann x/4 und - q/4

---

Ausklammern ist hier ganz falsch. Das Stichwort heißt 'binomische Formeln':

Ergänze zu einer binomischen Formel: x²+_x+16. Was gehört auf den Strich _?

---

Ich meine gerade beim ausklammern also bei anderen Aufgaben benutzt man bei polynomen jetzt in der PQ in der Wurzel bei beiden immer Bruch 4?

---

Meine Frage:   x²+_x+16.  Was gehört auf den Strich _?

hast du nicht beantwortet. Wenn du das nachholst, schreibe ich weiter.

---

Ja 8 müsste das sein ist ja die Aufgabe aber weiter weiß ich dort nicht wirklich auf die 4 komme ich nicht drauf wie man da drauf kommt

---

Okey habe es jetzt doch durch deine eklatant gut verstanden also geht sowas nur mit einer binomischen Formel ich denke in der Konstellation kommt es auch draun! Das man dann sieht die 4 geht ja auch in 8 und 16 das checkt man ja dann in der Arbeit, danke. Und wegen der x/4 in der Wurzel ist etwas komisch da er es manchmal macht x2,3 ist das und manchmal das normale x1,2

---

Schön, dass du mich verstanden hast. Umgekehrt war das nämlich nicht immer der Fall. Das liegt vor allem daran, dass du deine Kommentare abschickst, ohne sie noch einmal durchzulesen.

Falls du noch Fragen hast, bedenke das bitte.

Answer 3

Die Diskriminante der pq-Formel muss 0 ergeben:

(t/2)^2-16 = 0

t/2 = +-4

t = +-8

Answer 4

\(f(x)=x^2+t\cdot x+16\)

\(x^2+t\cdot x+16=0\)    quadratische Ergänzung:

\(x^2+t\cdot x+(\frac{t}{2})^2-\red{(\frac{t}{2})^2}+16=0\)    1.Binom:

\((x+\frac{t}{2})^2=\red{(\frac{t}{2})^2}-16    |\sqrt{~~}\)

\(x_1=- \frac{t}{2} + \sqrt{\red{(\frac{t}{2})^2}-16}\)

\(x_2=- \frac{t}{2} - \sqrt{\red{(\frac{t}{2})^2}-16}\)

Wenn genau eine Nullstelle gesucht wird, ist \( \sqrt{\red{(\frac{t}{2})^2}-16}=0\)

\( (\frac{t}{2})^2-16=0\)

\( \frac{t^2}{4}-16=0\)

\( t^2=64|\sqrt{~~} \)

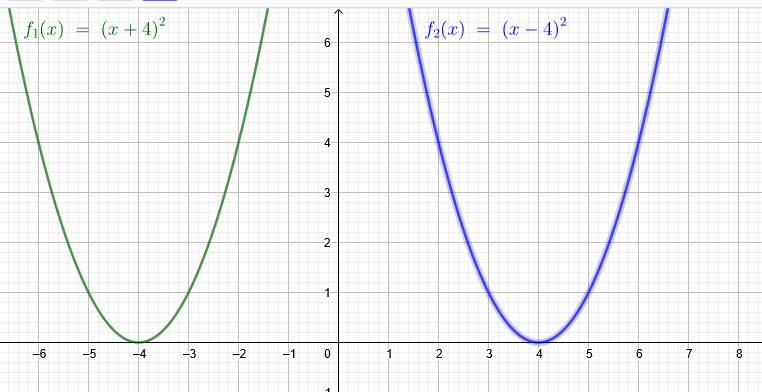
\( t_1=8\)            \(f_1(x)=x^2+8 x+16=(x+4)^2\)

\( t_2=-8\)        \(f_2(x)=x^2-8 x+16=(x-4)^2\)