Parameter bestimmen Folge ∞ .

Question

Text erkannt:

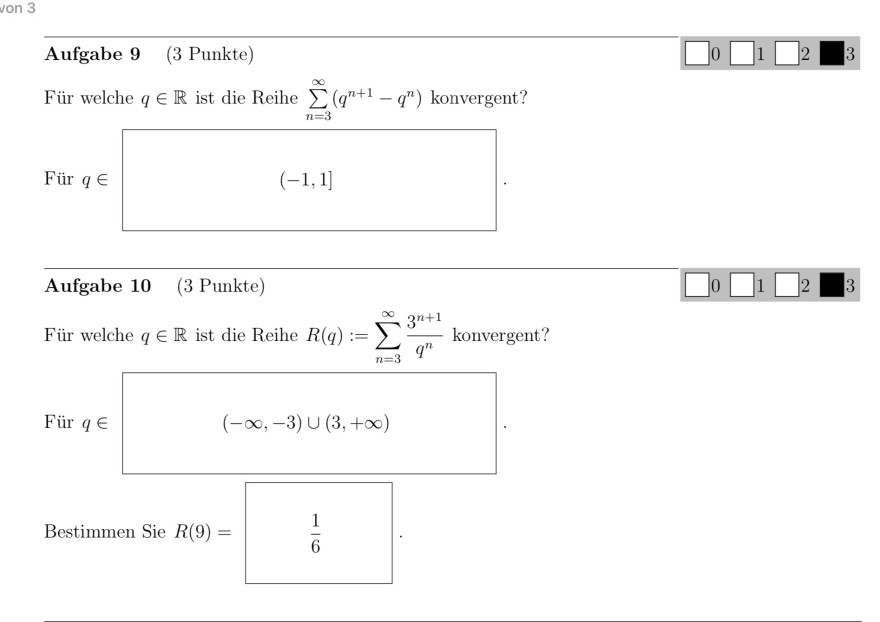
Aufgabe 9 (3 Punkte)
Für welche \( q \in \mathbb{R} \) ist die Reihe \( \sum \limits_{n=3}^{\infty}\left(q^{n+1}-q^{n}\right) \) konvergent?
Für \( q \in \quad(-1,1] \)

Aufgabe 10 (3 Punkte)
Für welche \( q \in \mathbb{R} \) ist die Reihe \( R(q):=\sum \limits_{n=3}^{\infty} \frac{3^{n+1}}{q^{n}} \) konvergent?

Für \( q \in \)
\( (-\infty,-3) \cup(3,+\infty) \)

Bestimmen Sie \( R(9)= \)
\( \frac{1}{6} \)

Aufgabe

Hallo, wie kann man die Parameter bestimmen? Bei 2 weiß ich dass der Wert zwischen 1 und -1 liegen muss aber bei 1 bin ich mir unsicher

Answer 1

q^(n + 1) - q^n = q^n·(q - 1)

Prinzipiell geht q^n gegen Null wenn -1 < q < 1 gilt. Dann brauchst du nur noch die Grenzen testen

für q = 1

1^n·(1 - 1) = 0

also kommt Null mit ins Intervall

für q = -1

(-1)^n·(-1 - 1) = (-1)^n·(-2)

Damit konvergiert die Reihe allerdings nicht.