Aufgabe: 3.1 Analysis Mathe LK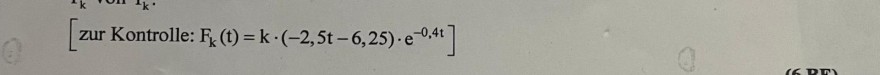
Text erkannt:
\( \left[\right. \) zur Kontrolle: \( \left.\mathrm{F}_{\mathrm{k}}(\mathrm{t})=\mathrm{k} \cdot(-2,5 \mathrm{t}-6,25) \cdot \mathrm{e}^{-0,4 \mathrm{t}}\right] \)

Text erkannt:
Landesabitur 2019
Hessisches Kultusministerium
Thema und Aufgabenstellung
Mathematik
Prüfungsteil 2 - Vorschlag B2
Leistungskurs (WTR)
3 Mit Nebelfängern (Material 2) lassen sich trockene Gebiete mit Trinkwasser versorgen. Der Nebel kondensiert an Folien, das Wasser sammelt sich und rinnt in Zisternen.
Die Sammelrate eines Nebelfängers vom Typ I kann durch geeignete Funktionen der Schar \( \mathrm{f}_{\mathrm{k}} \) aus Aufgabe 1, die Sammelrate eines Nebelfängers vom Typ II durch geeignete Funktionen der Schar \( g_{k} \) aus Aufgabe 2 modelliert werden.
Dabei gibt \( t \) mit \( t \in[0 ; 10] \) die nach 19 Uhr vergangene Zeit in Stunden an; \( f_{k}(t) b z w . g_{k}(t) \) gibt die Sammelrate des jeweiligen Nebelfängers in hundert Liter pro Stunde an.
Die Sammelrate des jeweiligen Nebelfängers hängt von unterschiedlichen Wetterlagen ab, welche mithilfe des Parameters \( \mathrm{k} \) mit \( \mathrm{k} \in[1 ; 3] \) modelliert werden können.
Unter der Ausbeute eines Nebelfangers versteht man die in der Zeit von 19 Uhr abends bis 5 Uhr morgens gesammelte Wassermenge.
3.1 Zeigen Sie, dass die Ausbeute eines Nebelfängers vom Typ I in hundert Liter in Abhängigkeit von \( \mathrm{k} \) durch die Funktion \( \mathrm{A}(\mathrm{k})=5,678 \cdot \mathrm{k} \) näherungsweise beschrieben wird.
Bestimmen Sie die minimal und die maximal mögliche Ausbeute eines Nebelfängers vom Typ I in Liter.
(4 BE)
Problem/Ansatz:
Den Beweis zu der Funktion hab ich bereits hergeleitet, aber mit dem zweiten Teil der Funktion habe ich keine Ahnung. Im Anhang oben finden sie die Stammfunktion von dem Nebelfänger Typ 1