Hallo,
mache Dir ein Bild! Ich habe Dir das Szenario in Desmos eingegeben:
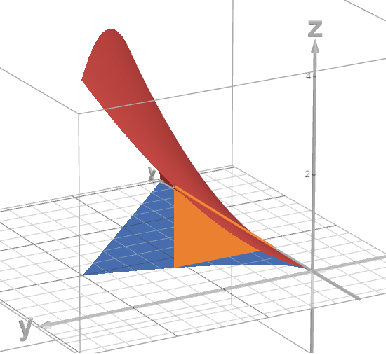
(klick auf das Bild, dann öffnet sich die Seite und Du kannst die Szene mit der Maus für einen besseren Eindruck rotieren)
Die blaue Fläche ist das Gebiet \(B\). Die rote Fläche ist der Graph der Funktion \(f(x,y)=xy/2\) über \(B\). Noch ein Tipp: Das gesuchte Integral entspricht dem Volumen über \(B\) unter der Funktion \(f(x,y)=xy/2\). Bevor Du das berechnest, schätze das Volumen ab. Du kannst es hier grob als Pyramide der Höhe 4 über einer dreieckigen Grundplatte mit \(G=6\cdot 4/2\) ansehen. D.h. beim Integral sollte in etwa 16 herauskommen (nur als Größenordnung).
Das orange Dreieck zeigt ein Volumenstück der Dicke \(\text{d}x\) unter \(f\). Diese orange Scheibe wird über \(y\) integriert, startet bei \(y=0\) und endet bei \(y=\min(x^2, 6-x)\). Und das ganze wird von \(x=0\) bis \(x=6\) aufsummiert. Alles zusammen:$$\begin{aligned} V &=\int\limits_{x=0}^{6} {\color{orange}\int\limits_{y=0}^{\min(x^2,6-x)}\frac{1}{2}xy\, \text{d}y}\text{d}x \\ &=\int\limits_{x=0}^{2} \,\int\limits_{y=0}^{x^2}\frac{1}{2}xy\, \text{d}y\text{d}x + \int\limits_{x=2}^{6} \,\int\limits_{y=0}^{6-x}\frac{1}{2}xy\, \text{d}y\text{d}x \\ &=\int\limits_{x=0}^{2} \left[\frac{1}{4}xy^2\right]_{y=0}^{x^2}\,\text{d}x + \int\limits_{x=2}^{6}\left[\frac{1}{4}xy^2\right]_{y=0}^{6-x}\,\text{d}x\\ &=\frac{1}{4}\left(\int\limits_{x=0}^{2}x^5\,\text{d}x + \int\limits_{x=2}^{6}x(6-x)^2\,\text{d}x\right)\\ &=\frac{1}{4}\left(\int\limits_{x=0}^{2}x^5\,\text{d}x + \int\limits_{x=2}^{6}36x-12x^2 + x^3\,\text{d}x\right)\\ &= \frac{1}{4}\left(\left[\frac{1}{6}x^6\right]_{x=0}^{2} +\left[18x^2-4x^3+\frac{1}{4}x^4\right]_{x=2}^{6}\right)\\ &= \frac{1}{4}\left(\frac{1}{6}\cdot 2^6 + 18\left(6^2-2^2\right) - 4 \left( 6^3-2^3\right)+ \frac{1}{4}\left(6^4-2^4\right) \right)\\&= \frac{56}{3} \end{aligned}$$Und falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner