Aufgabe:

Text erkannt:
5. \( (5+5+5+10=25 \) Punkte) Seien \( I \subset \mathbb{R} \) ein Intervall, das mindestens aus einem Punkt besteht und \( k \in \mathbb{N}_{0} \). Setze
\( C^{k}(I):=\{f: I \rightarrow \mathbb{R}: f \text { ist } k \text {-mal stetig differenzierbar }\} . \)
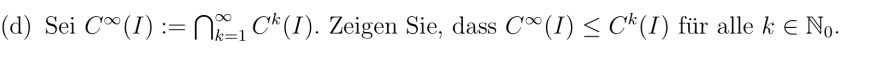
Text erkannt:
(d) Sei \( C^{\infty}(I):=\bigcap_{k=1}^{\infty} C^{k}(I) \). Zeigen Sie, dass \( C^{\infty}(I) \leq C^{k}(I) \) für alle \( k \in \mathbb{N}_{0} \).
Problem/Ansatz: Ich bin mir nicht sicher was genau ich zeigen soll. Soll ich zeigen, dass C(unendlich) untervektorraum von C(k) ist oder soll ich zeigen, dass c(k) mehr (gleich viele) Funktionen enthält ?