Finden Sie geeignete Geraden u, v, w ∈ G

Question

- Sie können die geforderten Graphiken auf Papier oder in GeoGebra
- Erläutern Sie Ihre Vorgehensweise im Zusammenhang mit dem Beweis von 7.13.

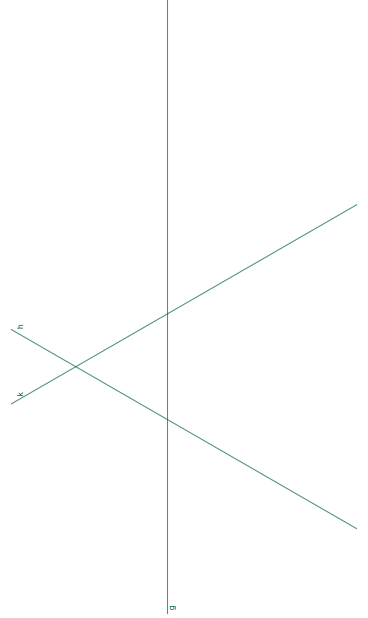
In den zugehörigen Graphiken (nächste Seiten) sind stets \( g, h, k \in \mathbb{G} \) gegeben. Nach 7.9 existieren \( u, v, w \in \mathbb{G} \) mit \( v \| w \) und \( u \perp v \), so dass: \( S_{g} \circ S_{h} \circ S_{k}=S_{u} \circ\left(S_{v} \circ S_{w}\right)=\left(S_{v} \circ S_{w}\right) \circ S_{u} \)

Finden Sie geeignete Geraden \( u, v, w \in \mathbb{G} \) wie oben und zeichnen Sie diese in die Graphik ein. Überprüfen Sie an einem Beispiel-Punkt \( X \in \mathbb{P} \), dass tatsächlich (wie gefordert) \( \left(S_{g} \circ S_{h} \circ S_{k}\right)(X)=\left(S_{u} \circ S_{v} \circ S_{w}\right)(X)=\left(S_{v} \circ S_{w} \circ S_{u}\right)(X) \) gilt.

Ich verstehe nicht ganz was ich tun soll. Ich weiß das ich Geraden finden soll an denen ich einen Punkt X spiegel aber was das Resultat davon sein soll verstehe ich nicht oder ich komme nicht drauf. Bitte um Erklärung was genau ich tun soll. Ebenfalls noch eine weitere Frage : Die Hintereinander Ausführungen lese ich ja immer Rückwärts oder ?

Answer 1

Das Resultat ist, dass die Spiegelungen immer den gleichen Bildpunkt liefern, was man auch sehen würde, wenn man es dann mal macht. Und ja, man fängt rechts an.

Comments

"Wenn man es dann mal macht" ich habe keine Lust auf schlechte Stimmung aber glaubst du wirklich wenn ich "es einfach so verstehen würde" müsste ich ein Forumsbeitrag schreiben? Scherzkeks.

---

Wo ist denn das Problem, einen Punkt zu spiegeln?

---

wenn ich beliebigen punkt X spiegel nach dem chema k->h->g wie kiege ich das hin das die spiegelungen an uvw und vwu gleich sind ?

---

Hast du dir den Beweis von 7.13 angeschaut? Offenbar dient das als Hilfe.

---

Ja nur leider beweist dieser nur den Satz 7.13 welcher lautet

Seien \( g, h, k \in \mathbb{G} \) und \( \Phi:=S_{g} \circ S_{h} \circ S_{k} \in \mathcal{K} \).
Dann existieren \( u, w, v \in \mathbb{G} \) mit \( v \| w \) und \( u \perp v \) (damit auch \( u \perp w \) ), so dass:
\( \Phi=S_{u} \circ\left(S_{v} \circ S_{w}\right)=\left(S_{v} \circ S_{w}\right) \circ S_{u} \)
- Im Fall \( v=w \) folgt \( \Phi=S_{u} \). In diesem Fall ist \( \Phi \) also eine Geradenspiegelung.
- Im Fall \( v \neq w \) nennt man \( \Phi \) eine Schubspiegelung (oder Gleitspiegelung).

---

Aber das ist ja genau das, was du möchtest. Ich gehe mal davon aus, dass der Beweis konstruktiv ist. Dass man ihm also entnehmen kann, wie man die Geraden konstruieren muss.

---

Ja jetzt hab ichs gerafft danke ! war ne geburt...

---

Das freut mich. :)