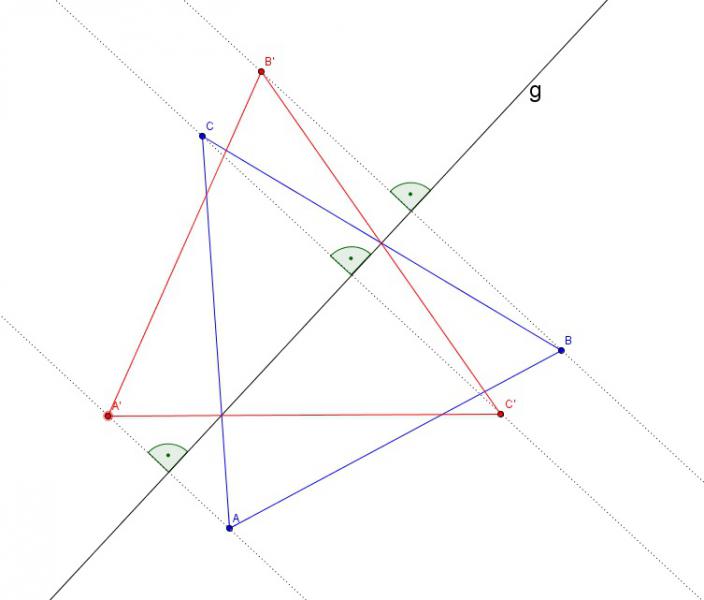
wir zeichnen ein beliebiges dreieck ABC.
wir zeichnen eine beliebige gerade durch das dreieck.
wir zeichnen hilfslinien, die durch die punkte A, B, C gehen
und senkrecht zur geraden sind.
wir übertragen die abstände der punkte A, B, C zur geraden g
auf die andere seite der geraden g entlang der hilfslinien.
damit bekommen wir die gespiegelten punkte des dreiecks,
die wir mit A', B' und C' bezeichnen.
die abstände lassen sich auch mit einem zirkel übertragen, ohne sie messen zu müssen.
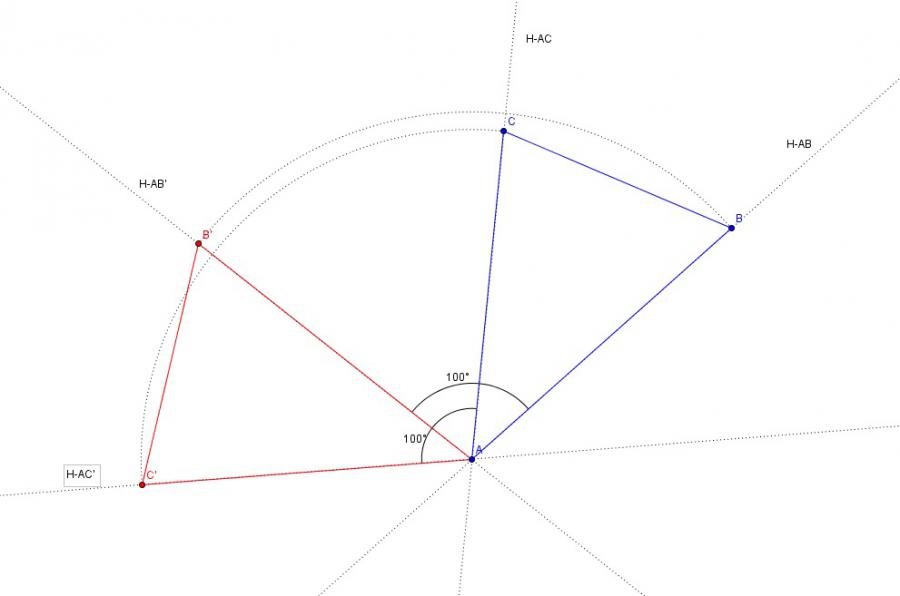
drehung des dreiecks ABC:
wir zeichnen ein beliebiges dreieck ABC.
wir zeichnen durch die punkte AB und AC eine
hilfsgerade H-AB und H-AC.
wir zeichnen zwei weitere hilfsgerade H-AB'
und H-AC'.
die gerade H-AB' hat einen winkel von
100° zur gerade H-AB und die gerade H-AC'
hat einen winkel von 100° zur gerade H-AC.
H-AB' und H-AC' verlaufen durch den punkt A,
weil A das drehzentrum ist.
jetzt brauchen wir nur noch den abstand AB
auf der hilfsgerade H-AB' vom drehzentrum A
einzutragen, das ergibt den punkt B'
und den abstand AC markieren wir auf der hilfsgerade
H-AC' und erhalten den punkt C'.
anstatt die punkte abzumessen, kann man auch mit einem
zirkel einen kreisbogen mit dem radius AB vom mittelpunkt A
zum schnittpunkt des kreisbogens mit H-AB' zeichnen, um
B' zu erhalten.
analog kann man mit dem zirkel den punkt C' ermitteln.
falls sich für dich noch fragen ergeben sollten, schreib es einfach als kommentar, ich werde gegen mittag wieder reinschauen.
lg