Hallo Max,
Willkommen in der Mathelounge!
Wir haben im Mathe mit kathetensatz angefangen ...
Na ja - dann weißt Du ja, dass das Quadrat über einer Kathete den gleichen Flächeninhalt hat, wie das Rechteck aus Hypotenuse und dem zugehörigen Hypotenusenabschnitt.
Wenn Du jetzt schon mal was vom Satz des Thales gehört hast und weißt, dass der Flächeninhalt des Parallelogramms nur von Grundseite und Höhe abhängt, so hast Du alles bei einander, was Du brauchst.
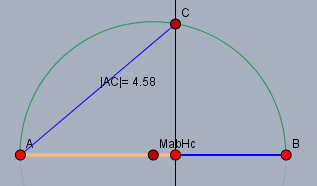
Zeichne die Strecke \(a=AB=6\,\text{cm}\) und darüber den Tahleskreis. Dann trage auf dieser Strecke die Höhe \(h_a=AH_c=3,5\,\text{cm}\) ab und errichte im Endpunkt dieser Strecke das Lot auf \(a\). Der Schnittpunkt des Lotes mit dem Thaleskreis sei \(C\). \(|AC|\) ist die gesuchte Seite des Quadrats.
Gruß Werner