Gleichungssystem praktisch lösbar?

Question

Folgendes Gleichungssystem liegt vor:

I: 5*a^2+5*b^2-2ab=1

II: 5*c^2+5*d^2-2*cd=1

III: 5*a*c-b*d- (a*d+b*c)=0

Ich finde irgendwie keine Lösung für die einzelnen Variablen auch wenn ich Annahmen anfangs treffe. Ist es überhaupt praktisch lösbar?

Comments

Das System ist unterbestimmt. 3 Gleichungen für 4 Unbekannte.

Daher kannst du eine Variable frei wählen.

Welche Annahmen hast du getroffen?

---

d=1 hätte ich zum Beispiel versucht

---

Nimm mal c= 0, siehe Mathecoach.

---

Die Klammerung in der letzten Gleichung kommt mir unmotiviert vor. Ist das ok?

---

Das ist kein lineares Gleichungssystem. Daher greifen die üblichen Methoden (Gleichungen/Unbekannte zählen, wieviele kann man frei wählen usw.) hier nicht.

---

Danke, das wusste ich so nicht.

Welche Methoden nimmt man stattdessen? Wie gehts am schnellsten ohne Technikeinsatz?

---

Es gibt für nichtlineare Gleichungssysteme keine allgemeingültigen Methoden oder Aussagen. Hängt vom Einzelfall ab.

---

Ich ahnte es. Danke nochmal.

---

@ nudger

Nur weil es kein lineares Gleichungssystem ist, ist es falsch zu behaupten, einer Variablen keinen festen Wert zuschreiben zu können. Im allgemeinen ist ein Gleichungssystem (ob linear oder nichtlinear) nicht eindeutig lösbar, falls mehr Unbekannte als Gleichungen vorliegen. Von daher ist es legitim, sich konkrete Werte anzuschauen, bei dem man eine Lösung bekommt.

---

Im allgemeinen ist ein Gleichungssystem (ob linear oder nichtlinear) nicht eindeutig lösbar, falls mehr Unbekannte als Gleichungen vorliegen.

Ist falsch. Die Gleichung \(x^2+y^2=0\) hat nur die Lösung \(x=y=0\). Wir haben hier aber offensichtlich mehr Unbekannte als Gleichungen.

---

Ja, das stimmt. Verbesserung: Ein Gleichungssystem (ob linear oder nichtlinear) ist nicht immer eindeutig lösbar, falls mehr Unbekannte als Gleichungen vorliegen. Bei deinem Beispiel hast du aber nur die reelle Lösung angegeben, denn \(y=i\cdot x\) ist auch eine Lösung von \(x^2+y^2=0\), wenn man komplexe Zahlen zulässt.

---

Die Aussage von nudger war übrigens nur, dass die gängigen Methoden nicht allgemeingültig sind. Er sagte ja auch, dass es eben vom Einzelfall abhängt.

---

@hallo97 ich hab nichts dergleichen behauptet.

---

Hier stets:

Daher greifen die üblichen Methoden (Gleichungen/Unbekannte zählen, wieviele kann man frei wählen usw.) hier nicht.

---

Das stimmt ja auch. Verstehst Du die Aussage nicht? Dass eine allgemeine Regel nicht gilt, heißt nicht, dass das Gegenteil der Regel gilt. Oder keine Ahnung was man sonst missverstehen könnte.

---

Dass eine allgemeine Regel nicht gilt, heißt nicht, dass das Gegenteil der Regel gilt.

Das habe ich nirgens gesagt.

Daher greifen die üblichen Methoden (Gleichungen/Unbekannte zählen, wieviele kann man frei wählen usw.) hier nicht.

Das ist eine sehr irreführende Formulierung, die einen dazu veranlässt, die dort genannten Punkte für diese Aufgabe erst garnicht mehr zu betrachten, erstrecht, die Erkenntnis auszunutzen, dass dieses Gleichungssystem hier unterbestimmt ist und man hier sehr wohl Variablen frei wählen kann.

---

Wozu Du Dich veranlasst fühlst, ist nun Deine Sache. Ich habe nur gesagt (nun zum 3. Mal), dass es auf dem Standardweg nicht geht. Das System hier ist nicht unterbestimmt (der Begriff greift nicht wie bei LGS) und man kann auch nicht einfach Variablen frei wählen (weil es kein LGS ist). Sieht man auch an der Lösung.

In Deiner Antwort bist Du ja auch gar nicht so vorgegangen.

---

Am Ende bekommst du auch auf meinem Weg die Erkenntnis, dass dieses System unendlich viele Lösungen hat.

Zumindest kann man das auch schon erahnen, wenn man weniger Gleichungen als Unbekannte hat.

---

Und das hast Du durchgerechnet? Dann leg mal vor.

Als Kostprobe reichen mir Deine Lösungen für c=1 und c=2.

Wir reden von reellen Lösungen, nur sicherheitshalber.

Answer 1

Hallo :-)

Du könntest zb die dritte Gleichung nach einer Variablen auflösen und den entstandenen Ausdruck in die beiden anderen einsetzen. Dann hast du somit nur noch zwei Gleichungen mit drei Unbekannten. Dann kannst du wieder nach einer Variablen auflösen. Beachte aber beim Umstellen nach einer Unbekannten, ob Probleme für spezielle Werte auftreten können, zb dass ein Ausdruck im Nenner Null wird, oder das Ausdrücke unter einer Wurzel negativ sind (falls du nur reelle Lösungen betrachten willst...). Die Werte, die eben diese Probleme mit sich bringen, musst du dann gesondert betrachten und damit das Ausgangs-Gleichungssystem neu betrachten.

Answer 2

Musst du das denn von Hand lösen?

Wirf das doch einfach mal Wolframalpha zum Fraß vor.

https://www.wolframalpha.com/input?i=5a%5E2%2B5b%5E2-2ab%3D1%2C5c%5E2%2B5d%5E2-2cd%3D1%2C5ac-bd-%28ad%2Bbc%29%3D0

$$a=-\frac{1}{2 \sqrt{3}}, \quad b=\frac{1}{2 \sqrt{3}}, \quad c=0, \quad d=-\frac{1}{\sqrt{5}}$$

Comments

Na ja ist eine Probeklausuraufgabe, demnach schon ja

---

Klausur-in welchem Fach?

---

"Lineare Modelle". Das Gleichungssystem stammt eigentlich aus einer Aufgabe wo ich eine Zufallsvariable transformieren muss.

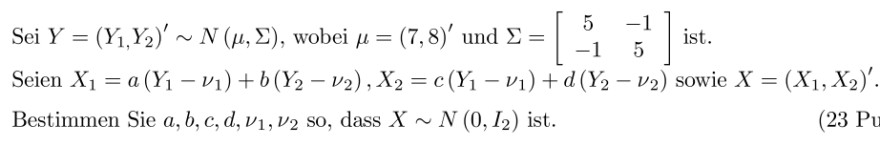
Text erkannt:

Sei \( Y=\left(Y_{1}, Y_{2}\right)^{\prime} \sim N(\mu, \Sigma) \), wobei \( \mu=(7,8)^{\prime} \) und \( \Sigma=\left[\begin{array}{cc}5 & -1 \\ -1 & 5\end{array}\right] \) ist.
Seien \( X_{1}=a\left(Y_{1}-\nu_{1}\right)+b\left(Y_{2}-\nu_{2}\right), X_{2}=c\left(Y_{1}-\nu_{1}\right)+d\left(Y_{2}-\nu_{2}\right) \) sowie \( X=\left(X_{1}, X_{2}\right)^{\prime} \).
Bestimmen Sie \( a, b, c, d, \nu_{1}, \nu_{2} \) so, dass \( X \sim N\left(0, I_{2}\right) \) ist.

---

Dann ist dein LGS definitiv falsch und du brauchst dafür auch kein LGS, wenn du die Transformationsformel benutzt.

---

Ok, dann weiß ich zmd mal das. Danke für den Hinweis!

---

Oh Mann. Oh Mann. Das war ja mal wieder eine tolle "Aufgabenstellung"

---

Ich finde es durchaus in Ordnung, wenn die Fragesteller nur Teilprobleme liefern, an denen sie hängen. Das zeigt zumindest, dass sie sich mit den Aufgaben schon auseinandergesetzt haben und nicht für eine bestimmte Aufgabe gleich die komplette Lösung wollen/brauchen.

Wie gut, dass man hier Fragen stellen kann und eben nicht immer nur Aufgaben reinklatschen muss. :)

---

Ein Satz zur Einordnung der Fragestellung würde reichen und helfen. Es gibt genug Beispiele hier und überall, wo sich solche Teilfragen als Ente erwiesen haben

---

@Mathhilf ich nehme es zur Kenntnis und werde es in Zukunft genauer ausführen (:

---

@Battel101
Schau mal hier.

---

Es läuft aber immer darauf raus, dass man ein Gleichungssystem hat bestehen aus der Varianz bzw. Kovarianz hat

---

Nein, hat man nicht. Kommt dir ein Ausdruck wie \(A\Sigma A^T=D\) nicht bekannt vor? Stichwort Diagonalisierbarkeit von Matrizen.

---

ASO, daran habe ich gar nicht gedacht. Vielen Dank