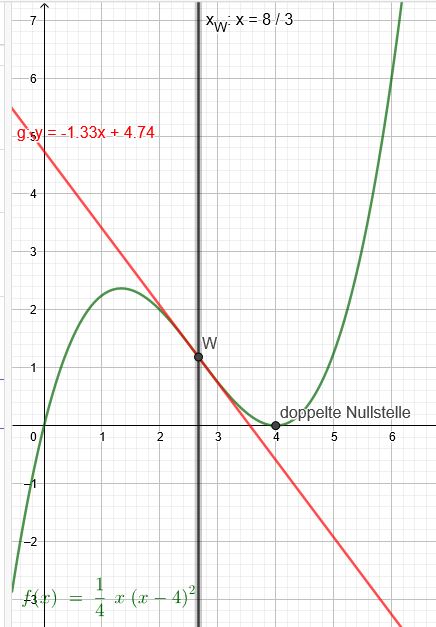
Eine ganz rationale Funktion 3. Grades hat bei \(x_N = 4\) eine doppelte Nullstelle und bei \(x_W = \frac{8}{3}\) ihre Wendestelle. Die Tangente im Wendepunkt des Graphen hat die Steigung m=\(-\frac{4}{3}\)
Weg über die Nullstellenform der kubischen Parabel:
\(f(x)=a(x-N_1)(x-N_2)(x-N_3)\)
bei \(x_N = 4\) eine doppelte Nullstelle:
\(f(x)=a(x-4)(x-4)(x-N_3)=a[(x-4)^2(x-N_3)]\)
Tangentensteigung im Wendepunkt m=\(-\frac{4}{3}\)
\(f'(x)=a[(2x-8)(x-N_3)+(x-4)^2 ]\)
\(f'(\frac{8}{3})=a[(-\frac{8}{3})(\frac{8}{3}-N_3)+\frac{16}{9}]=-\frac{4}{3} \)
\(a[(-\frac{64}{9})+\frac{8}{3}N_3+\frac{16}{9}]=-\frac{4}{3} \)
\(a[(-\frac{48}{9})+\frac{8}{3}N_3]=-\frac{4}{3} \)
\(a[(-\frac{12}{9})+\frac{2}{3}N_3]=-\frac{1}{3} \)
\(a[(-\frac{4}{3})+\frac{2}{3}N_3]=-\frac{1}{3} \)
\(a[(-4+2N_3]=-1 \)
\(a[(4-2N_3]=1 \) → \(a=\frac{1}{4-2N_3} \)
\(f'(x)=\frac{1}{4-2N_3}[(2x-8)(x-N_3)+(x-4)^2 ]\)
\(f''(x)=\frac{1}{4-2N_3}[(2x-2N_3)+(2x-8)+(2x-8) ]\)
\(f''(\frac{8}{3})=\frac{1}{4-2N_3}[(2\cdot\frac{8}{3}-2N_3)+(4\cdot\frac{8}{3}-16)]\)
\(\frac{1}{4-2N_3}[(2\cdot\frac{8}{3}-2N_3)+(4\cdot\frac{8}{3}-16)]=0\)
\(N_3=0\)
\(a=\frac{1}{4} \)
\(f(x)=\frac{1}{4}x(x-4)^2\)