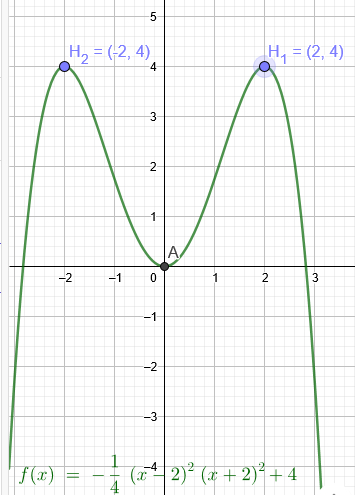
"Der Graph einer ganzrationalen Funktion 4. Grades ist achsensymmetrisch, verläuft durch den Ursprung uns hat einen Hochpunkt bei H(2|4)."
Ich verschiebe den Graphen um 4 Einheiten nach unten:
H₁´(2|0) H₂´(-2|0)
f(x)=a*(x-2)^2*(x+2)^2
U´(0|-4)
f(0)=a*(0-2)^2*(0+2)^2
16a=-4
a=-\( \frac{1}{4} \)
f(x)=-\( \frac{1}{4} \)*(x-2)^2*(x+2)^2
Nun 4 Einheiten nach oben:
f(x)=-\( \frac{1}{4} \)*(x-2)^2*(x+2)^2+4