Fundamentalsystem partikuläre und allgemeine Lösung

Question

Aufgabe:

(i) Bestimmen Sie ein Fundamentalsystem von

\( y^{\prime}=\left(\begin{array}{cc} 0 & -4 \\ 1 & 4 \end{array}\right) y \)

und geben Sie damit die allgemeine Lösung von

\( y^{\prime}=\left(\begin{array}{cc} 0 & -4 \\ 1 & 1 \end{array}\right) y+\left(\begin{array}{c} 1-t) \mathrm{e}^{2 t} \\ 0 \end{array}\right) \)

Problem/Ansatz:

Fundamentalsystem gelöst, wasw ist der Ansatz für die partikuläre Lösung und damit die allgemeine Lösung?

Comments

Wahrscheinlich sollst du doch üben, was Ihr in der Vorlesung besprochen habt. Möglich wär e

1. Variation der Konstanten mit dem berechneten Fundamentalsystem

2. Rückführung auf den 1-dim Fall

Ob es bei Systemen so etwas wie "Ansatz vom Typ der rechten Seite" gibt, weiß ich nicht.

Answer 1

Hallo,

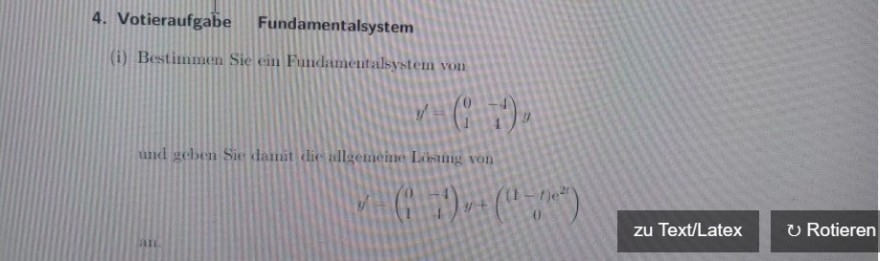
Lösung via Variation der Konstanten:

\( \begin{array}{l}y^{\prime}=\left(\begin{array}{cc}0 & -4 \\ 1 & 4\end{array}\right) y+\left(\begin{array}{cc}(1-t) e^{2 t} \\ 0\end{array}\right) \\ y_{h}=\left(\begin{array}{cc}-2 e^{2 t} & (-2 t+1) e^{2 t} \\ e^{2 t} & t e^{2 t}\end{array}\right)\end{array} \)

(Fundamentalsystem)

\( \begin{array}{l}y_{p}=y(t) \cdot\left(\begin{array}{l}c_{1}(t) \\ c_{2}(t)\end{array}\right) \\ y_{p}^{\prime}=y^{\prime}(t) \cdot\left(\begin{array}{l}c_{1}(t) \\ c_{2}(t)\end{array}\right)+y(t)\left(\begin{array}{l}c_{1}^{\prime}(t) \\ c_{2}^{\prime}(t)\end{array}\right)\end{array} \)

\( \left(\begin{array}{cc}-2 e^{2 t} & (-2 t+1) e^{2 t} \\ e^{2 t} & t e^{2 t}\end{array}\right)\left(\begin{array}{l}c_{1}^{\prime} \\ c_{2}^{\prime}\end{array}\right)=\left(\begin{array}{c}(1-t) e^{2 t} \\ 0\end{array}\right) \)

\( \begin{array}{l}y^{-1}(t)=\frac{1}{\operatorname{det}(A)}\left(\begin{array}{cc}d & -b \\ -c & a\end{array}\right) \\ y^{-1}(t)=\frac{1}{-e^{4 t}}\left(\begin{array}{cc}t e^{2 t} & (2 t-1) e^{2 t} \\ -e^{2 t} & -2 e^{2 t}\end{array}\right) \\ y^{-1}(t)=\left(\begin{array}{cc}-t e^{-2 t} & (-2 t+1) e^{-2 t} \\ e^{-2 t} & 2 e^{-2 t}\end{array}\right) \\ \left(\begin{array}{l}c_{1} ^{\prime}\\ {c_2}^{\prime}\end{array}\right)=\left(\begin{array}{cc}-t e^{-2 t} & (-2 t+1) e^{-2 t} \\ e^{-2 t} & 2 e^{-2 t}\end{array}\right)\left(\begin{array}{c}\left(1-t) e^{2 t}\right. \\ 0\end{array}\right)\end{array} \)

 ------->Falksches Schema:

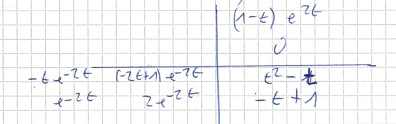
\( \begin{array}{l}c_{1}(t)=\int\left(t^{2}-t\right) d t=\frac{t^{3}}{3}-\frac{t^{2}}{2} \\ c_{2}(t)=\int(-t+1) d t=-\frac{t^{2}}{2}+t \\\end{array} \)

--------------------------------------------------------------------------------------------------------------

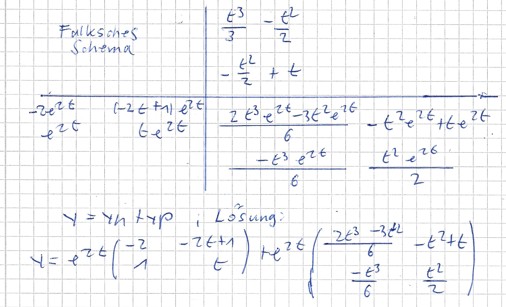
2.Möglichkeit:

Beim "Ansatz mittels der rechten Seite" lautet dieser für die partikuläre Lösung:

yp₁=t (a t+b) e^(2t)

yp₂=t (A t+B) e^(2t)

-> Resonanz

dann yp1 und yp2 jeweils 1 Mal ableiten und in die beiden DGL vom System einsetzen.

Anschließend einen Koeffizientenvergleich tätigen.

y=yh +yp