3x3 Matrix Eigenwert, Eigenvektoren, Lösung des Differenzialgleichungssystems zum Anfangswert

Question

hey ich hätte noch eine frage hierzu:

ich muss die Eigenvektoren dieser Matrix bestimmen:

 

Die Eigenwerte lauten λ₁=0 , λ₂=5 und λ₃=-5

Für λ₁ kommt eingesetzt das hier raus:

 

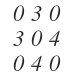
Mit dem Kreuzproduktverfahren habe ich nun die folgenden Vektoren zur Auswahl:

 

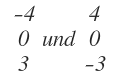
die sind ja im Grunde das -1 -fache des anderen... ABER

Wenn ich die Lösung des Differenzialgleichungssystems suche zu z.B. dem Anfangswert x(0) = (1, −1, −2)^t dann

wird, je nachdem welches ich davon nehme, ein anderes Ergebnis kommen? Da ich ja was anderes für die Konstante C bekomme?

ist das egal was ich nehme?

 

Answer 1

um den Eigenvektor zu λ₁ =0 zu bekommen löst man die Gleichung

Ax=0 (x ist ein Vektor).

man erhält dann als Lösung

x=(t,0,-3t/4) , t∈ℝ

Du kannst einen beliebigen Eigenvektor des Eigenraums heraussuchen, sie unterschieden sich lediglich durch einen Vorfaktor. Dieser Vorfaktor wird aber dann durch die Konstante C₁ absorbiert.

Bsp: es ist egal ob ich schreibe C₁ * (1,0,0)=-1*C₁ *(-1,0,0) =: C₂ *(-1,0,0)

Comments

klasse... ich war echt verwirrt wegen dieser sache und habe nix dazu gefunden... danke nochmal