Überdeckung eines Rechtecks

Question

ABCD und EFGH seien Quadrate. FAJG ist ein Rechteck. F und A liegen auf EB, J liegt auf EC. Mit welchen Anzahlen von Quadraten kongruent zu EFGH kann das Rechteck FAJG überschneidungsfrei und vollständig überdeckt werden, damit die Fläche des Sechsecks EBCDJH ein natürliches Vielfaches der Dreiecksfläche EFC ist?

Comments

ich habe mal gelesen, dass die wahrscheinlichste Lösung bei Gleichungen mit \(x\) aus der Schule die Lösung $$x=5$$ ist. Also wenn ich hier raten müsste, wäre das mein Favorit. ;-)

---

Lieber Werner, x=5 ist leider nicht richtig. Zwei Lösungen findet man mit Mittelstufenkenntnissen. Schwieriger ist der Beweis, dass dies die einzigen sind.

---

y=2*(x+1+1/x) hat in natürlichen Zahlen nur die Lösungen x=1 und x=2

---

x=5 ist leider nicht richtig.

Oh ja - 5 war eine mögliche Anzahl der Quadrate im Sechseck FBCDJG ...

---

"5 war eine mögliche Anzahl der Quadrate im Sechseck FBCDJG"

Werner, kannst du mir sagen, wie das zur (richtigen) Lösung von hj2166 passt?

---

Werner, kannst du mir sagen, wie das zur (richtigen) Lösung von hj2166 passt?

in \(y=2\left(x+1+\frac{1}{x}\right)\) ist \(x\) die Strecke \(|FA|\) (im Verhältnis zu \(|EF|\)) und \(y\) das Verhältnis der Flächen von \(EBCDJH\) zum \(\triangle EFC\) . Die Gleichung hat in \(\mathbb{N}\) die Lösungen \(x\in\{1,\,2\}\) und für \(x=1\) gibt sich folgendes Bild:

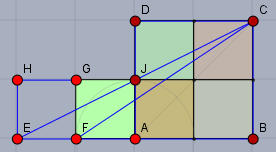
Das Sechseck \(FBCDJG\) kann in diesem Fall mit \(5\) Quadraten \(EFGH\) abgedeckt werden.

Ich hatte mich so intensiv mit der Ortslinie des Punktes \(C\) beschäftigt (einer Hyperbel), dass ich darüber die genaue Aufgabenstellung vergessen hatte. Daher die Verwirrung.