Bestimmen Sie eine Gleichung der Tangentialebene der Funktion f an der Stelle

Question

Aufgabe:

Tangentialebene bestimmen mit bestimmtem Punkt und partielle Ableitungen

Problem/Ansatz:

Ist meine Lösung richtig? Ich habe die Tangentialebene noch nicht berechnet, aber ich bin mir sowieso mit den Antworten davor nicht sicher. Kann mir jemand helfen?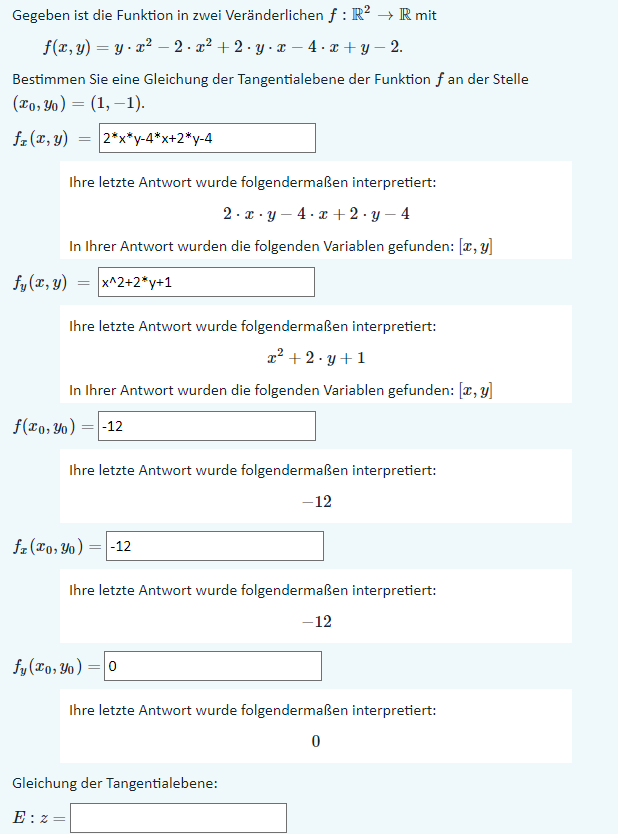

Text erkannt:

Gegeben ist die Funktion in zwei Veränderlichen \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) mit
\( f(x, y)=y \cdot x^{2}-2 \cdot x^{2}+2 \cdot y \cdot x-4 \cdot x+y-2 . \)

Bestimmen Sie eine Gleichung der Tangentialebene der Funktion \( f \) an der Stelle
\( \begin{array}{l} \left(x_{0}, y_{0}\right)=(1,-1) \\ f_{x}(x, y)=2^{*} x^{*} \mathrm{y}-4^{*} \mathrm{x}+2^{*} \mathrm{y}-4 \end{array} \)

Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( 2 \cdot x \cdot y-4 \cdot x+2 \cdot y-4 \)

In Ihrer Antwort wurden die folgenden Variablen gefunden: \( [x, y] \)
\( f_{y}(x, y)=\mathrm{x}^{\wedge} 2+2^{*} \mathrm{y}+1 \)

Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( x^{2}+2 \cdot y+1 \)

In Ihrer Antwort wurden die folgenden Variablen gefunden: \( [x, y] \)
\( f\left(x_{0}, y_{0}\right)=-12 \)

Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( -12 \)
\( f_{x}\left(x_{0}, y_{0}\right)=-12 \)

Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( -12 \)
\( f_{y}\left(x_{0}, y_{0}\right)=0 \)

Ihre letzte Antwort wurde folgendermaßen interpretiert:
0
Gleichung der Tangentialebene:
\( E: z= \)

Answer 1

Aloha :)

Wir formen den Funktionsterm kurz um, damit wir einfacher rechnen können:$$f(x;y)=x^2y-2x^2+2xy-4x+y-2$$$$\phantom{f(x;y)}=(x^2y+2xy+y)-(2x^2+4x+2)$$$$\phantom{f(x;y)}=y\cdot(x^2+2x+1)-2\cdot(x^2+2x+1)$$$$\phantom{f(x;y)}=y\cdot(x+1)^2-2\cdot(x+1)^2$$$$\phantom{f(x;y)}=(y-2)(x+1)^2$$

Damit sind die Ableitungen klar:$$f_x(x;y)=2(y-2)(x+1)$$$$f_y(x;y)=(x+1)^2$$

Speziell an der Stelle \((x_0;y_0)=(1;-1)\) erhalten wir:$$f_x(1;-1)=-12\quad;\quad f_y(x;y)=4\quad;\quad f(1;-1)=-12$$

Die Gleichung der Tangentialebne lautet daher:$$z=f(x_0;y_0)+f_x(x_0;y_0)\cdot(x-x_0)+f_y(x_0;y_0)\cdot(y-y_0)$$$$\phantom z=f(1;-1)+f_x(1;-1)\cdot(x-1)+f_y(1;-1)\cdot(y-(-1))$$$$\phantom z=-12+(-12)\cdot(x-1)+4\cdot(y+1)$$$$\phantom z=-12x+4y+4$$