Aufgabe: Hallo,
die Aufgabenstellung steht auf dem Bild und ich habe auch schon einen Ansatz gemacht, ich will mir nur sicher gehen ob das so richtig ist.
Danke im Voraus
Problem/Ansatz:
Den Ansatz habe ich gemacht auf den zwei anderen Bildern habe ich die Lösung von A und y_0 notiert, dabei habe ich erstmal den Vektor
y = (y1,y2,y3)^T aufgeschrieben.
Somit habe ich weiter
y1 = u
y1‘ = y2 = u‘
y2‘ = y3 = u“
y3‘ = u‘‘‘ = 3y3 - 2y2 + 5y1
geschrieben, somit kam ich auf y_0 und A.
Ist das so richtig? 
Text erkannt:
Zur Lösung einer Differentialgleichung
\( u^{(n)}(t)+\sum \limits_{i=0}^{n-1} a_{i} u^{(i)}(t)=0 \)
mit gegebenen Anfangswerten \( u^{(i)}(0)=u_{0}^{i}, i=0, \ldots, n-1 \), transformiert man dieses durch die Wahl \( y(t)=\left(\begin{array}{c}u(t) \\ \vdots\end{array}\right) \) in ein System erster Ordnung
\( y^{\prime}(t)=A y(t), \quad y(0)=y_{0} . \)
(a) Zur Lösung der Differentialgleichung \( u^{\prime \prime \prime}(t)-3 u^{\prime \prime}(t)+2 u^{\prime}(t)-5 u(t)=0 \) mit Anfangswerten \( u^{\prime \prime}(0)= \) \( 4, u^{\prime}(0)=2 \) und \( u(0)=-3 \) erhält man
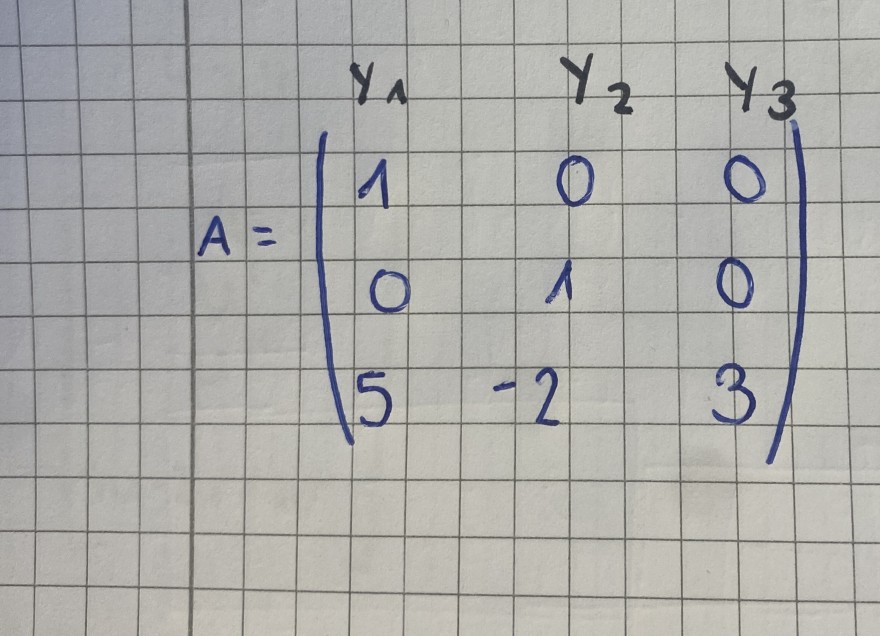
Text erkannt:
\( A=\left(\begin{array}{ccc}y_{1} & y_{2} & y_{3} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 5 & -2 & 3\end{array}\right) \)
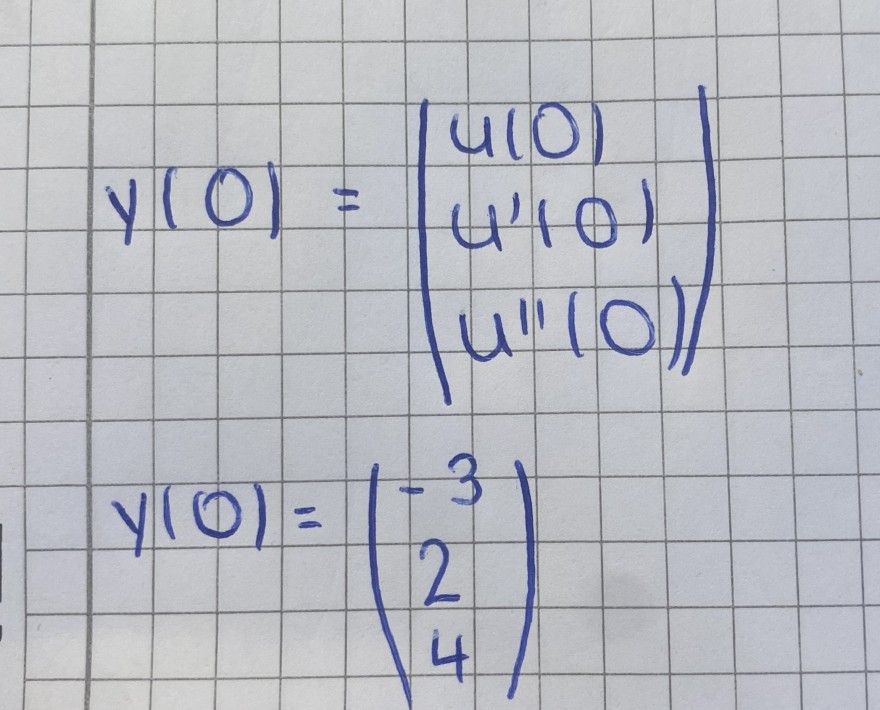
Text erkannt:
\( \begin{array}{l}y(0)=\left(\begin{array}{l}u(0) \\ u^{\prime}(0) \\ u^{\prime \prime}(0)\end{array}\right) \\ y(0)=\left(\begin{array}{c}-3 \\ 2 \\ 4\end{array}\right)\end{array} \)