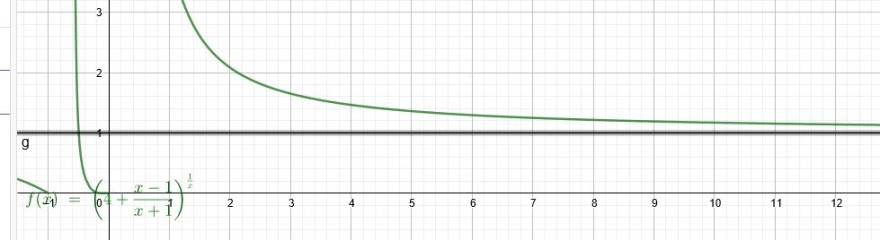
Unter der \(\sqrt[n]{~~} \) steht:
\({4 + \frac{n-1}{n+1}} ={\frac{4n+4+n-1}{n+1}} ={\frac{5n+3}{n+1}}={\frac{\frac{5n}{n}+\frac{3}{n}}{\frac{n}{n}+\frac{1}{n}}}={\frac{5+\frac{3}{n}}{1+\frac{1}{n}}}\)
\( \lim\limits_{n\to\infty}=5 \)
\(\sqrt[n]{5} =1\)