Aufgabe:

Text erkannt:
Consider the function \( f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R} \) given by
\( f(x)=\frac{81}{x^{3}}-\frac{3}{x} \)
For any \( x \in \mathbb{R} \backslash\{0\} \), the first and second derivatives are given by
\( f^{\prime}(x)=\frac{3 x^{2}-243}{x^{4}} \)
and
\( f^{\prime \prime}(x)=\frac{972-6 x^{2}}{x^{5}}, \)
respectively.
The two zeros \( z_{1}, z_{2} \) of the first derivative are -9 and 9 , the zeros \( z_{3} \) and \( z_{4} \) of the second derivative are approximately -12.73 and 12.73 , respectively. Furthermore, the (one-sided) limits at \( -\infty, \infty \) and 0 are
\( \begin{array}{l} \lim \limits_{x \rightarrow-\infty} f(x)=0, \\ \lim \limits_{x \rightarrow \infty} f(x)=0, \\ \lim \limits_{x>0} f(x)=-\infty, \end{array} \)
and
\( \lim \limits_{x \searrow 0} f(x)=\infty . \)
Complete the following text so that true statements result.
Text erkannt:
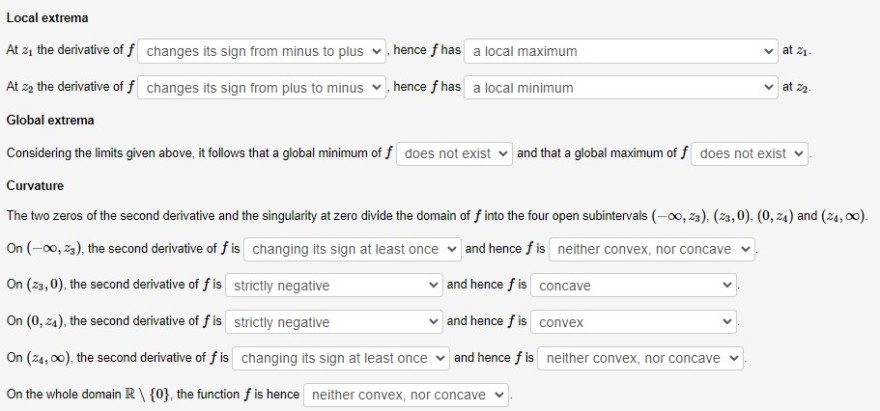
Local extrema
At \( z_{1} \) the derivative of \( f \) changes its sign from minus to plus \( \checkmark \), hence \( f \) has a local maximum \( \quad \checkmark \) at \( z_{1} \).
At \( z_{2} \) the derivative of \( f \) changes its sign from plus to minus \( \vee \), hence \( f \) has a local minimum \( \quad \) at \( z_{2} \).
Global extrema
Considering the limits given above, it follows that a global minimum of \( f \) does not exist \( \checkmark \) and that a global maximum of \( f \) does not exist \( \checkmark \).
Curvature
The two zeros of the second derivative and the singularity at zero divide the domain of \( f \) into the four open subintervals \( \left(-\infty, z_{3}\right),\left(z_{3}, 0\right),\left(0, z_{4}\right) \) and \( \left(z_{4}, \infty\right) \).
On \( \left(-\infty, z_{3}\right) \), the second derivative of \( f \) is changing its sign at least once \( \checkmark \) and hence \( f \) is neither convex, nor concave \( \vee \).
On \( \left(z_{3}, 0\right) \), the second derivative of \( f \) is strictly negative \( \quad \checkmark \) and hence \( f \) is concave
On \( \left(0, z_{4}\right) \), the second derivative of \( f \) is strictly negative \( \quad \checkmark \) and hence \( f \) is convex
On \( \left(z_{4}, \infty\right) \), the second derivative of \( f \) is changing its sign at least once \( \checkmark \) and hence \( f \) is neither convex, nor concave \( \checkmark \).
On the whole domain \( \mathbb{R} \backslash\{0\} \), the function \( f \) is hence neither convex, nor concave \( \checkmark \).
"Changes its sign from minus to plus" und das andere sind falsch oder ist die Curvature Aufgabe da unter falsch?
VG