Mit
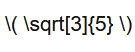
geht es.
Logarithmus Funktionen und Exponentialfunktion lösen
Ich finde in der Aufgabe übrigens keine Funktion und erst recht keine Exponentialfunktion.
Was da steht, ist eine Gleichung. Nicht einmal eine, die man nach x auflösen müsste, denn das ist sie schon. Es ist auch keine Logarithmusgleichung.