Fakultät und Potenzen

Question

kann mir jemand erklären im Detail, warum hier n! * n zu n! wird?

n! * (n+1) = (n+1)! kenne ich. Würde gerne verstehen warum n! * n = n!  n! ist doch auch = (n-1)*n! oder?

Warum wird n^n * (n+1)^n zu (n+1)^n   Das potenzgesetz besagt a^n * b^n = (a*b)^n Warum ist n^n * (n+1)^n = (n+1)^n???

Danke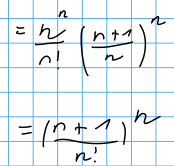

Text erkannt:

\( \begin{array}{l}=\frac{n^{n}}{n !}\left(\frac{n+1}{n}\right)^{n} \\ =\left(\frac{n+1}{n !}\right)^{n}\end{array} \)

Text erkannt:

\( \begin{array}{l}=\frac{n}{n !}\left(\frac{n+1}{n}\right)^{n} \\ =\left(\frac{n+1}{n !}\right)^{n}\end{array} \)

Answer 1

Du solltest den Term im Gesamten betrachten und nicht Zähler und Nenner einzeln: Das \(n^n\) kürzt sich doch sofort raus. $$\frac{n^n}{n!}\cdot \left(\frac{n+1}{n}\right)^n=\frac{\red{n^n}}{n!}\cdot \frac{(n+1)^n}{\red{n^n}}$$

Comments

Danke Apfelmännchen für die Antwort. Langsam bekomme ich einen Blick dafür. Tausend Dank!