Nullstellen der Funktion ermitteln?

Question

Aufgabe: Wenn man bei der Funktion die Nullstellen ermitteln will? Kann man nach diesem Weg vorgehen?

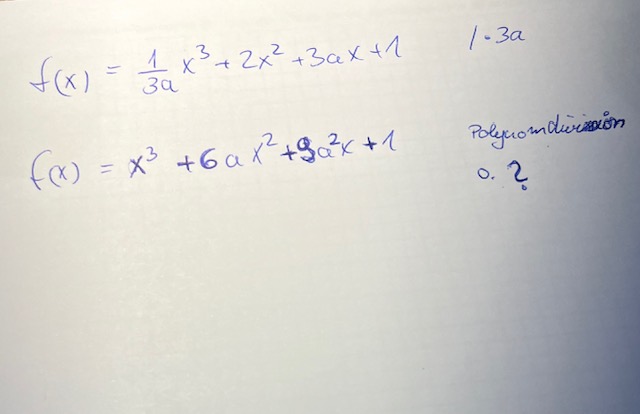
Text erkannt:

$f(x)=\frac{1}{3 a} x^{3}+2 x^{2}+3 a x+1 \quad 1-3 a$
$f(x)=x^{3}+6 a x^{2}+9 a^{2} x+1$

Polynomdirizion
0. ?

Oder gibt es da noch einen anderen Ansatz?

Problem/Ansatz: Hallo Leute, bei der Ermittlung der Nullstellen komme ich gerade nicht weiter. Kann ich die Polynomdivision nutzen, um die Nullstellen zu ermitteln? Falls sich jemand auskennt, bitte kleinen Anstoß geben;) Danke für die Zeit.

mfg

Comments

Ersetze erst einmal die 1 am Ende durch 3a.

---

Es gäbe dazu eine Formel:

https://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/cardani…

In diesem Fall eher etwas für Masochisten.

Du kannst die Lösung nur in Abhängigkeit von a angeben.

---

Danke schön für die Hilfe.

---

Hallo

pass auf beim Multiplizieren mit a auf also a≠0  da der Term vorher ja für a=0 nicht definiert ist.

Da man keine Nst raten kann, ist das sicher keine aufgabe, da niemand verlangt sowas allgemein zu lösen, für Zahlenwerte von a nutzt man dann Näherungsverfahren.

Woher stammt denn die Aufgabe?

lul

---

Aus einer Altklausur muss man Wendepunkt ermitteln, dazu brauche ich ja Nst. um in die 3 Ableitung einzusetzen.

---

Für Wendepunkte brauchst du die Nullstellen der 2. Ableitung.

---

Hallo

Wenn das die Fkt ist, ist die Gleichung für die einzige Wendestelle doch eine lineare Funktion? deren Nullstelle ist leicht zu finden bei x=-2a

warum sollte man die Nst in die dritte Ableitung einsetzen?

Gruß lul

---

Die Nst von $f''$ muss man schon durch Einsetzen in $f'''$ prüfen, denn, sollte $f'''(-2a)=0$ sein, ist nicht klar, dass dort ein WP vorliegt. Hier ist aber $f'''(-2a)\neq 0$, also liegt in der Tat dort ein WP vor.

Answer 1

$f(x)=\frac{1}{3 a} x^{3}+2 x^{2}+3 a x+1 \quad |\cdot 3 a$

Dann bekommst du die Gleichung

        $3a\cdot f(x) = x^{3}+6ax^{2}+9 a^2 x+3a$