Question

Scheitelpunktform und allgemeine Form der Parabeln bestimmen:
1. $S(6 / 4), P(3 /-14)$
2. $S(-3 /-2), P(1 / 6)$
3. $S(4 / 12), P(2 / 0)$

Comments

Vor vier Jahren waren deine Fragen deutlich anspruchsvoller.

Answer 1

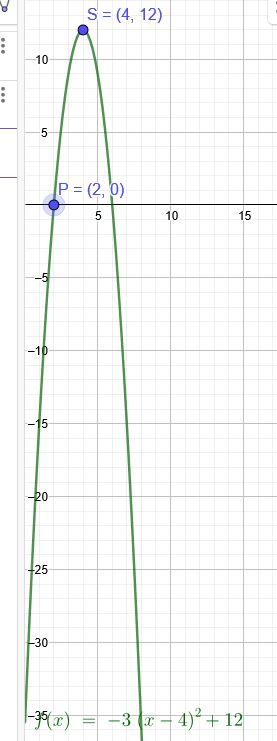
Die Scheitelpunktform der Parabel lautet:

$f(x)=a\cdot (x-x_S)^2+y_S$

$S(4 | 12)$

$f(x)=a\cdot (x-4)^2+12$

$P(2 | 0)$

$f(2)=a\cdot (2-4)^2+12=4a+12$

$4a+12=0$→ $a=-3$

$f(x)=-3\cdot (x-4)^2+12$

Die allgemeine Form findest du mit dem Ausmultiplizieren.

Answer 2

Allgemein

a = (Py - Sy) / (Px - Sx)²

f(x) = a·(x - Sx)² + Sy = a·(x² - 2·Sx·x + Sx²) + Sy = a·x² - 2·a·Sx·x + a·Sx² + Sy

1.

a = (-14 - 4) / (3 - 6)² = -18 / 9 = -2

f(x) = -2·(x - 6)² + 4 = -2·(x² - 12x + 36) + 4 = -2·x² + 24x - 68

Answer 3

Hallo

man sollte wissen die Scheitepunktform mit dem Scheitel(xs,ys)'

y=a(x-xs)²+ys

1. Scheitelpunktform du setzt den Scheitel ein, dann in die Gleichung den Punkt und bestimmst so a.

2. dann umformen u, die allgemeine Formel y=ax²+bx+c zu finden

fertig-

gruß lul