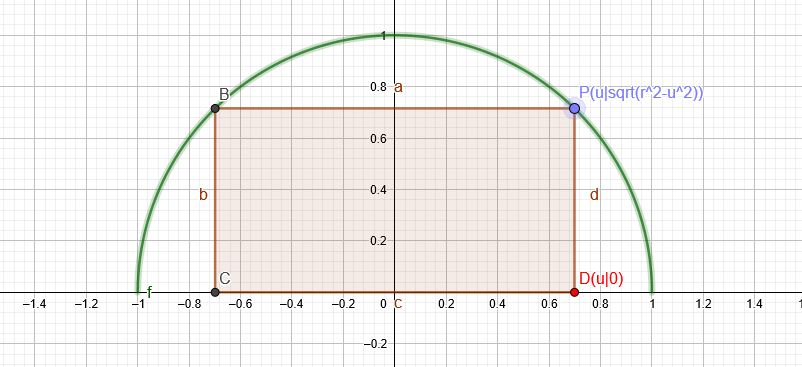
\(A(u)=2u\cdot f(u)\) soll maximal werden.
\(f(u)= \sqrt{r^2-u^2} \)
\(A(u)=2u\cdot \sqrt{r^2-u^2}=\sqrt{4u^2(r^2-u^2)}=\sqrt{4u^2\cdot r^2-4u^4}\)
\(A'(u)=\frac{8r^2u-16u^3}{2\sqrt{4u^2\cdot r^2-4u^4}}=\frac{4r^2u-8u^3}{\sqrt{4u^2\cdot r^2-4u^4}}\)
\(\frac{4r^2u-8u^3}{\sqrt{4u^2\cdot r^2-4u^4}}=0\)
\(r^2u-2u^3=0\)
\(u(r^2-2u^2)=0\)
\(u_1=0\)
\(r^2-2u^2=0\)
\(u^2=\frac{1}{2}r^2\)
- entfällt:
\(u=\frac{1}{2}\sqrt{2} \cdot r\)
\(l=\sqrt{2} \cdot r\)
\(f(u)=b= \sqrt{r^2-\frac{1}{2}r^2}=\frac{1}{2}\sqrt{2} \cdot r \)