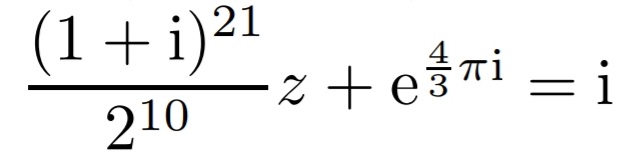
Text erkannt:
\( \frac{(1+\mathrm{i})^{21}}{2^{10}} z+\mathrm{e}^{\frac{4}{3} \pi \mathrm{i}}=\mathrm{i} \)
Aufgabe:
Bestimmen Sie die algebraische Darstellung sowie die Exponentialdarstellung der komplexen Zahl z, die
\( \frac{(1+i)^{21}{(2^{10}} \)*z+e\( x^{\frac{4}{3}}*π*i\)=i
erfüllt!
Problem/Ansatz:
Komme leider nicht weiter als dass man evtl nach z umstellt. Danke im voraus!