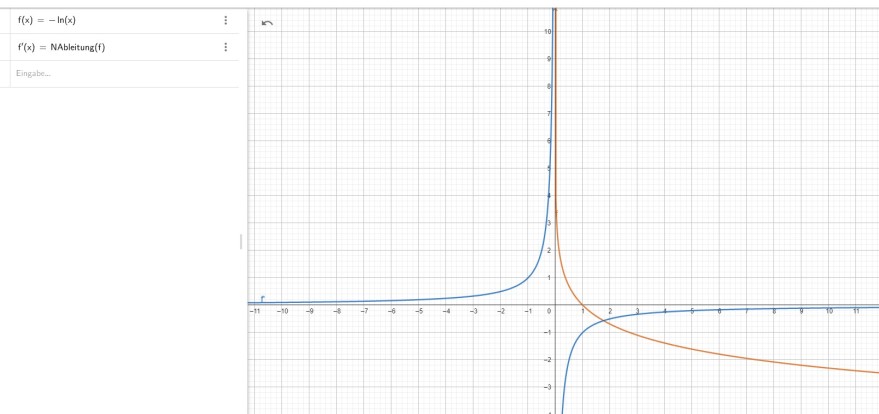
Aufgabe:
Ich soll zeigen dass im Intervall ]0;unendlich[
die Funktion streng monoton fallend ist.
Problem:
Das Intervall bedeutet ja dass die Werte 0 und unendlich nicht streng monoton ist.
aber f'(x) ist von 0 bis unendlich negativ.. bedeutet ja das f(x) da auch streng monoton fallend oder?
Und da f'(-1) im positiven ist, müsste es ja bedeuten, dass f(-1) steigend ist?
Allerdings erkennt man die negativen x-Werte von f(x) nicht.. es geht nur von x=0 bis x=unendlich