Hallo,
eine Gleichung 3. Grades und ihre ersten beiden Ableitungen kannst du so darstellen:
\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f''(x)=6ax+2b\\\)
Für die vier Unbekannten a, b c und d brauchst du 4 Gleichungen. Die Informationen dazu entnimmst du dem Aufgabentext.
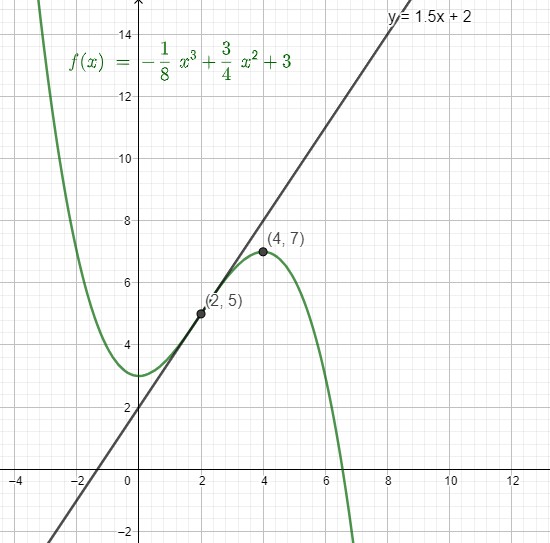
Extremstelle bei x = 4. Das bedeutet \(f'(4)=0\), denn die Steigung an einer Extremstelle ist null.
Wendestelle bei x = 2. Das bedeutet \(f''(2)=0\), denn die notwendige Bedingung für eine Wendestelle ist, dass die 2. Ableitung null ist.
Wendetangente y = 1,5x + 2
1,5 ist die Steigung an dieser Stelle, also \(f'(2)=1,5\)
Die y-Koordinate des Wendepunktes kannst du berechnen, indem du 2 für x in die Tangentengleichung einsetzt:
\(y=1,5\cdot 2+2=5\), also \(f(2)=5\)
Damit lautet das Gleichungssystem
\(f'(4)=0\Rightarrow 48a+8b+c=0\\ f''(2)=0\Rightarrow 12a+2b=0\\ f'(2)=1,5\Rightarrow 12a+4b+c=1,5\\ f(2)=5\Rightarrow 8a+4b+2b+d=5\)
Das brauchst du jetzt nur noch zu lösen und/oder dich melden, falls du noch Fragen hast.
Gruß, Silvia