Aufgabe:
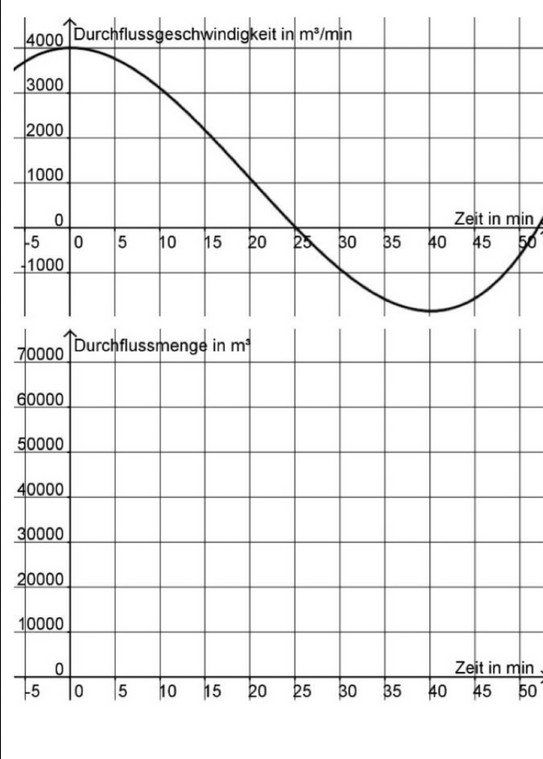
In der Abbildung rechts ist das Füllen und Entleeren eines Pumpspeicherwerkes mit nichtkonstanter Zuflussgeschwindigkeit dargestellt.
(I) Bestimmen Sie näherungsweise anhand des Graphen, um wie viel m3 sich die Wassermenge im oberen Becken im Zeitraum von 25, 40 und 50 Minuten geändert hat.
(II) Skizzieren Sie unter dem Graphen in dem neuen Koordinatensystem qualitativ den Graphen des Wasserbestandes im oberen Becken für den Fall, dass es zum Zeitpunkt 0 leer ist. Begründen Sie seinen Verlauf. Erläutern Sie insbesondere die Bedeutung von Extrem- und Nullstellen des oberen Graphen für den unteren Graphen.
(III) Wie ändert sich der Graph der Bestandsfunktion, wenn sich zu Beginn 10.000 m3 Wasser im oberen Becken befinden?
Problem/Ansatz:
Ich bräuchte Unterstützung bei den Aufgaben weil ich steh gerade echt auf dem Schlauch