Berechnen Sie die Determinante einer 5x5 Matrix?

Question

Aufgabe: Berechnen Sie die Determinante!

Problem/Ansatz:

Ich bin mir nicht sicher ob es schlau ist, immer wieder die neu berechnete Formel zu berechnen, um dann auf eine 2x2 Matrix zu kommen.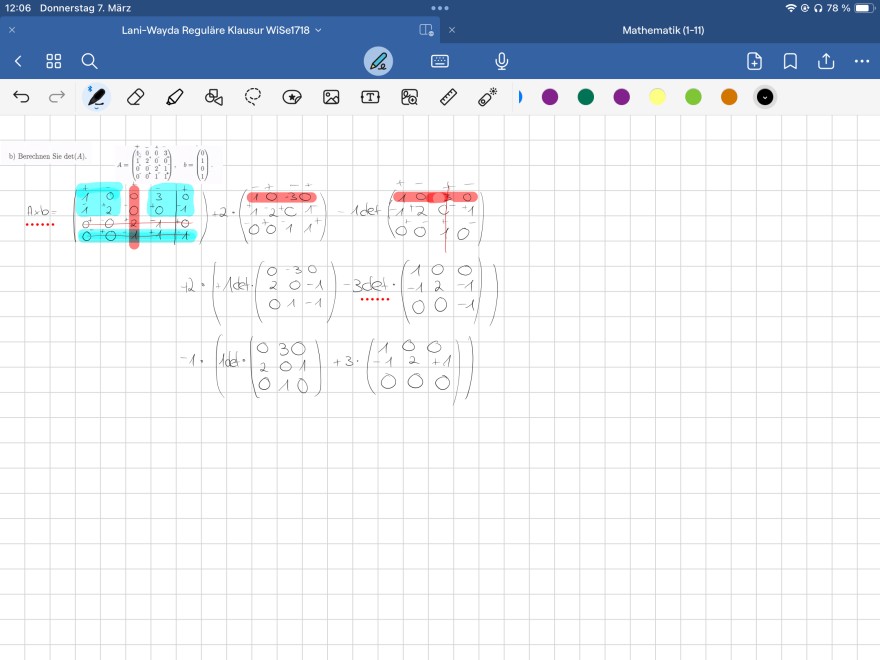

Text erkannt:

b) Berechnen Sie \( \operatorname{det}(A) \)
\( A=\left(\begin{array}{cccc} 1 & 0 & 0 & 3 \\ 1 & 2^{+} & 0 & 0 \\ 0^{-} & 0^{+} & 2^{+} & 1 \\ 0^{-} & 0^{+} & 1^{\prime} & 1^{2} \end{array}\right), \quad b=\left(\begin{array}{l} 0 \\ 1 \\ 0 \\ 1 \end{array}\right) \text {. } \)
\( \begin{array}{l} -1 \cdot\left(1 \mathrm{de} \cdot\left(\begin{array}{lll} 0 & 3 & 0 \\ 2 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right)+3 \cdot\left(\begin{array}{ccc} 1 & 0 & 0 \\ -1 & 2 & +1 \\ 0 & 0 & 0 \end{array}\right)\right) \\ \end{array} \)

Comments

Für mich sieht das so aus, als würdest Du versuchen aus einer 4-5-Matrix eine Determinante auszurechnen. Das ist aber nicht definiert.

Die Aufgabe verlangt det(A)

---

Die Matrix ist eine Blockdreiecksmatrix. Es gilt

$$ \det \begin{pmatrix} A_{11} &\dotsm& \dotsm & A_{1n}\\ 0 & A_{22} & & \vdots\\ \vdots & \ddots & \ddots & \vdots \\ 0 &\dotsm &0 & A_{nn} \end{pmatrix} = \prod_{i=1}^n \det(A_{ii})$$

Answer 1

Hallo

ich sehe nur eine 4 mal 4 Matrix, mit 2 0 eintragen in der ersten Zeile und Spalte, d,h. man hat nur 2 einfache 3 mal 3 Matrizen zu berechnen, Das kann man direkt nach sarrus oder eben fast genau so einfach mit 2 mal 2 Untermatrizen. Deine Untermatrizen verstehe ich nicht ganz. Da stehen 4 Untermatrizen, du brauchst doch nur 2 die zu 1 in der ersten Zeile und die mit 3 .dabe streichst du jeweils die Zeile  und Spalte in der die 1 bzw. der 3.  die Untermatrizen haben wieder so viel Allen, das nur 1 bzw 2 2*2 Matrizen rauskommen. Also was genau ist die Frage, dein Zettel ist eigenartig. Es gibt matrizenrechner im Netz, mit denen du dein Ergebnis überprüfen kannst, die Zeigen auch den Rechenweg an  etwa https://matrixcalc.org/de/ oder https://matrix.reshish.com/de/determinant.php

Gruß lul