Begründen, dass Volumen größer

Question

Aufgabe:

Text erkannt:

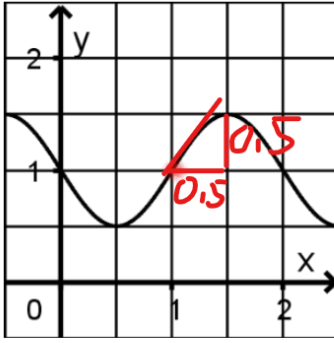
Die Abbildung zeigt den Graphen einer in IR definierten Funktion \( \mathrm{f} \).
a Beurteilen Sie die folgende Aussage:
Für jeden Wert von \( x \) mit \( 0 \leq x \leq 2 \) ist die Steigung des Graphen von \( f \) kleiner als 3.
b Mit dem Term \( \pi \cdot \int \limits_{0}^{2}(f(x))^{2} d x \) kann das Volumen eines Körpers berechnet werden. Begründen Sie, dass dieses Volumen größer als \( \pi \cdot 0,5^{2}+\pi \cdot 1^{2} \) ist.

bei der a) Habe ich bei der Wendestelle x=1 ein Steigungsdreieck zum Hochpunkt gemacht und die Steigung ist aufjedenfall kleiner als 3.

bei der b) bitte ich um Hilfe, da ich keine Idee habe, wie ich das zeigen soll.

Also mir ist klar, dass das Integral das Volumen angibt von 0 bis 2 also die Fläche unterm Graphen geschlossen durch die x-Achse. Ich weiß nicht, welche Grenzen beim Term pi*0,5^2 + pi*1^2  genutzt wurden.

Falls die Grenze bei dem Term zb von x=0 bis x=3 wäre.. dann ist das Volumen logischerweise größer als von 0 bis 2.

Wie erkenne ich hier die genutzten Grenzen des Terms und gibt es eine andere Möglichkeit?

Text erkannt:

\( \pi \cdot 0,5^{2}+\pi \cdot 1^{2} \)

Answer 1

Du brauchst die Grenzen gar nicht zu kennen, da du das Volumen berechnen kannst. Betrachte mal genau die vom Graphen eingeschlossene Fläche. Kannst du sie berechnen? Wenn ja, kannst du auch das Volumen des Rotationskörpers berechnen. Das geht dann mit Hilfe eines Zylinders. ;)

Comments

Ohh verdammt, ich wäre nie draufgekommen.

Ich war mir sehr sicher, dass der Term pi*0,5^2 + pi*1^2 durch kleinere Grenzen entstanden wäre und dadurch das Volumen kleiner ist. Aber wahrscheinlich kann man die Grenzen nicht aus dem Term bekommen.

Also "Du brauchst die Grenzen gar nicht zu kennen, da du das Volumen berechnen kannst" ohne Grenzen bedeutet kein Integral. Hmmm..

also Zylinder lässt sich mit V= pi*r^2*h berechnen.

h ist hier 2(?) weil Grenzen von 0 bis 2 gehen. Radius ist dann 1..

Dadurch könnte ich V berechnen.

Eine Frage noch: Bei Flächen- oder Volumenberechnung mit Funktionen, ziehe ich immer nur das Integral in Betracht.

Es kommt mir vor als hätte ich Wissenslücken aber braucht man bei solchen Aufgaben immer Berechnung mit Körpern?

---

Das Integral ist ja auch nicht grundsätzlich falsch. Man sollte aber einfach auch andere Möglichkeiten in Erwägung ziehen, gerade wenn man symmetrische Funktionen hat. Da ist dann natürlich vorteilhaft, wenn man das Volumen von diversen Körpern berechnen kann.

Übrigens zum Zustandekommen des Terms: Der erste Summand ist der Zylinder mit dem Radius 0,5 und der zweite Summand der Zylinder mit dem Radius 1. Mit dem Integral wurde hier gar nichts berechnet. Beide "Rechtecke" für die Rotation liegen unterhalb des Graphen von f.