Aufgabe:
Text erkannt:
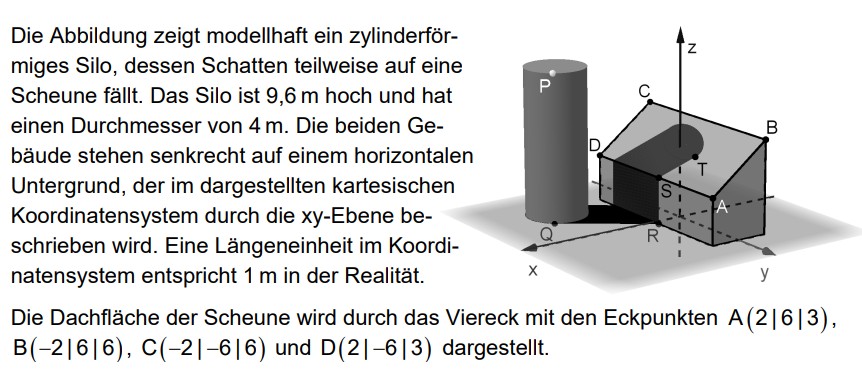
Die Abbildung zeigt modellhaft ein zylinderförmiges Silo, dessen Schatten teilweise auf eine Scheune fällt. Das Silo ist \( 9,6 \mathrm{~m} \) hoch und hat einen Durchmesser von \( 4 \mathrm{~m} \). Die beiden Gebäude stehen senkrecht auf einem horizontalen Untergrund, der im dargestellten kartesischen Koordinatensystem durch die \( x y \)-Ebene beschrieben wird. Eine Längeneinheit im Koordinatensystem entspricht \( 1 \mathrm{~m} \) in der Realität.
Die Dachfläche der Scheune wird durch das Viereck mit den Eckpunkten \( A(2|6| 3) \), \( \mathrm{B}(-2|6| 6), \mathrm{C}(-2|-6| 6) \) und \( \mathrm{D}(2|-6| 3) \) dargestellt.

Text erkannt:
Das Sonnenlicht, das zu einem bestimmten Zeitpunkt auf die beiden Gebäude trifft, kann durch parallele Geraden mit dem Richtungsvektor \( \left(\begin{array}{c}-4 \\ 3 \\ -3\end{array}\right) \) beschrieben werden. Der Raumbereich zwischen Silo und Scheune, der vom Sonnenlicht nicht erreicht wird, wird von mehreren Flächen begrenzt. Eine dieser Begrenzungsflächen wird durch das ebene Fünfeck PQRST beschrieben, wobei der Punkt \( T \) im Modell den Schatten von \( \mathrm{P}(7,2|-3,4| 9,6) \) darstellt.
e Das Fünfeck PQRST liegt in der Ebene F. Begründen Sie ohne die Koordinaten eines weiteren Eckpunkts des Fünfecks zu bestimmen, dass \( F \) durch die Gleichung \( 3 x+4 y=8 \) beschrieben wird.
f Berechnen Sie die Länge der Strecke \( \overline{\mathrm{ST}} \).
g Eine zweite Begrenzungsfläche des betrachteten Raumbereichs liegt im Modell in einer Ebene \( \mathrm{H}: 3 x+4 y=d \) mit \( d \in \mathbb{R} \). Berechnen Sie den Wert von \( d \).
Ich habe eine Frage zur g)
Was ist hier die zweite Begrenzungsfläche, ich kann diese nicht erkennen.
Kann mir jemand beschreiben, wo diese zu finden ist und ob diese parallel zum Fünfeck PQRST ist?
Vielen Dank,
LG