Volumen & Blickrichtung Saarpolygon

Question

Aufgabe:

ich habe zwei Fragen zu den Aufgaben

und es geht NUR UMS VISUELLE.

Ich habe mehrmals probiert bei GeoGebra den Quader zu zeichnen

und die Pyramide dazu, allerdings stürzt die Seite ab, sobald ich ein Körper

gezeichnet habe und das zweite zeichnen will.

1) Einmal würde ich gerne unbedingt sehen, dass die Grundfläche der Pyramide hier 1/2 der Grundfläche

des Quaders entspricht. Und weshalb die Höhe der Pyramide gleich der Höhe des Quaders ist.

Von wo muss ich draufschauen, weil ich erkenne das nicht.

2) Abbildung 3 verstehe ich. Aber Abbildung 4 erkenne ich nicht, wie man das sieht.

Es soll wohl vom Vektor BC sein. Also ich sehe das Dreieck nur wenn ich ABC betrachte.

Aber dann wüsste ich nicht warum nur der Vektor BC die Blickrichtung ist und A nicht im Vektor ist.

*Entschuldigung hier die Ebene E:

Die Kontrollgleichung ist E.

Und Die Pyramide ABC

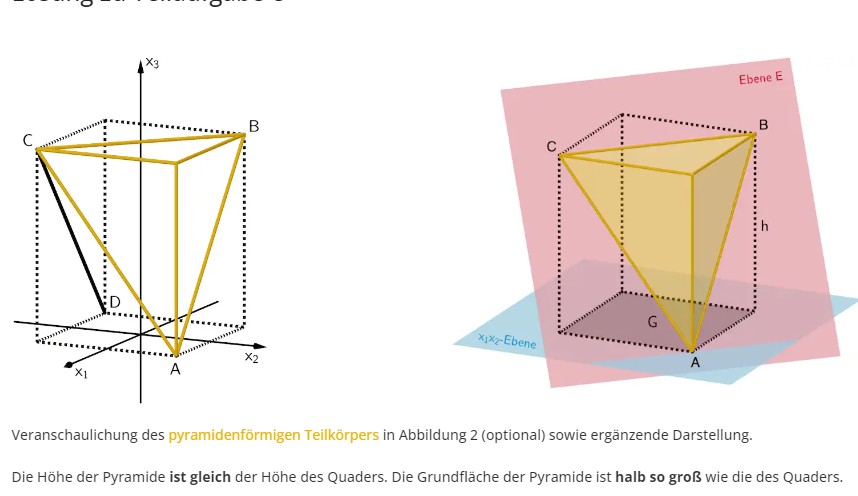
Text erkannt:

Veranschaulichung des pyramidenförmigen Teilkörpers in Abbildung 2 (optional) sowie ergänzende Darstellung.

Die Höhe der Pyramide ist gleich der Höhe des Quaders. Die Grundfläche der Pyramide ist halb so groß wie die des Quaders.

Quelle: https://www.mathelike.de/abiturloesungen-mathematik-bayern/mathematik-abitur-bayern-2022/pruefungsteil-b/geometrie-2/teilaufgabe-e.html

Vielen Dank,

LG

Answer 1

Aber dann wüsste ich nicht warum nur der Vektor BC die Blickrichtung ist und A nicht im Vektor ist.

3 Punkte in einem Vektor? Beachte, dass es die Blickrichtung ist. Ein Dreieck beschreibt keine Richtung. Du schaust also von der hinteren rechten Ecke auf das Bauwerk.

Für die andere Frage ist leider unklar, um welche Ebene und welche Pyramide es geht.

Die Grundfläche der Pyramide setzt sich zusammen aus dem Dreieck mit den Punkten A, C und der vorderen oberen Ecke. Die Höhe ist dann die Länge des Quaders, die nach hinten geht.

Comments

Entschuldigung, ich habe die Frage nun bearbeitet.

Text erkannt:

\( \bigwedge^{c} \)

Ist es also falsch, wenn ich das Dreieck von dieser Sicht sehe:

---

Das was du siehst, ist das Dreieck ABD oder ACD. Die Kante BC kannst du nicht sehen, weil das deine Blickrichtung ist.

Habe die Antwort zur Pyramide ergänzt.

---

Text erkannt:

Ebene E
\( x_{1} x_{2} \)-Ebene
C
B
8
h

Ouhh jetzt sehe ich es, danke danke :)

Also das ist die Grundfläche.

Und eine Frage noch zur Höhe:

Text erkannt:

Ebene E

jede orangene Linien stellt die Höhe dar. Diese wäre ja überall gleich lang oder?

Bzw. die Höhe könnte man ja auch aus dem Mittelpunkt der Grundfläche herausfinden,

wenn diese zur Spitze geht:

Text erkannt:

Ebene E
C

---

Nein. Die Höhe steht senkrecht auf der Grundfläche. Deine markierten Seiten sind also nicht alle die Höhe. Und nach Pythagoras können sie nicht gleich lang sein.

---

"Die Höhe ist dann die Länge des Quaders, die nach hinten geht."

Ich denke also ist das die Höhe:

Text erkannt:

Ebene E
C

Weil es geht von der rechten oberen Ecke nach hinten zu B.. meinst du das? Aber das wäre ja nicht die senkrechte Höhe der Grundfläche

---

Die meine ich. Warum ist die Höhe nicht senkrecht zur Grundfläche der Pyramide?

---

Ouh verdammt, ich habe gedacht, die Höhe wäre über den Mittelpunkt.so wie bei der Pyramide.

Aber darum gehts ja nicht, sondern hauptsache die Höhe ist senkrecht und nicht eine seitliche Höhe.

Danke, jetzt habe ich es endlich :)

---

Das freut mich. :)