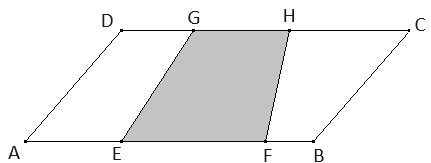
Gesucht ist der Flächeninhalt eines Parallelogramms ABCD, nachdem bekannt ist, dass der Flächeninhalt eines Trapezes EFHG mit derselben Höhe den Flächeninhalt 40 hat und außerdem gilt \(2| \overline{EF} |=| \overline{AB}|\) und \(3| \overline{GH} |=| \overline{DC} |\).