Wie groß ist die Steigung der Tangente im Punkt B?

Question

Aufgabe:

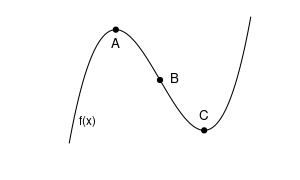
Die folgende Grafik zeigt drei kritische Punkte der Funktion f(x) bzw. ihrer Ableitung f'(x) . Die Funktion ist gegeben durch:

f(x) = 1,13x³ - 2,59x² - 1,14x - 1,17

Wie groß ist die Steigung der Tangente im Punkt B?

Problem/Ansatz:

Ich habe es folgendermaßen berechnet und bin mir nicht sicher ob es stimmt.

f(x) = 1,13x³ - 2,59x² - 1,14x - 1,17

f'(x) = 3,39x² - 5,18x - 1,14

f''(x) = 6,78x - 5,18

Danach die 2te Ableitung 0 setzten

x1= -0,877610699

x2= -5,902389301

und zum Schluss x1-x2 = 5,024778602

Ist das Ergebniss richtig? Danke für jede Hilfe!

Answer 1

\(f(x) = 1,13x^3 - 2,59x^2 - 1,14x - 1,17\)

\(f'(x) = 3,39x^2 - 5,18x - 1,14\)

\(f''(x) = 6,78x - 5,18\)

\( 6,78x - 5,18=0\)

Wendestelle bei \(≈0,76\)

Steigung der Wendetangente:

\(f'(0,76) = 3,39\cdot 0,76^2 - 5,18\cdot 0,76- 1,14≈-3,12\)

Answer 2

Hallo,

Danach die 2te Ableitung 0 setzten

Bis hierhin ist alles richtig. Bei dem Graphen der 2. Ableitung handelt es sich um eine Gerade. Zwei Nullstellen sind daher nicht möglich, sondern nur eine (s. Antwort von Moliets).

und zum Schluss x1-x2 = 5,024778602

Wie kommst du denn darauf? Kann es sein, dass du Formel für die Steigung einer Geraden durch zwei gegebene Punkte im Kopf hattest \(\bigg(m=\frac{y_1-y_2}{x_1-x_2}\bigg)\) und diese großzügig auf den Nenner reduziert hast?

Merke dir für zukünftige Aufgaben dieser Art: Steigung = 1. Ableitung

Gruß, Silvia

Comments

Hallo, also ich habe die 2te Ableitung Null gesetzt und das händisch mit dieser Formel berechnet:

Text erkannt:

\( x_{1,2}=-\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^{2}-q} \)

Ich dachte ich müsste danach die Differenz von x1 und x2 berechnen und ich hätte das Ergebnis. Also um alles nochmal zusammenzufassen: Ich setze die 2te Ableitung 0, und setzte dann das Ergebnis in die 1te Ableitung und so hab ich die Steigung der Tangente B, ist das richtig so?

LG

---

So ist es. Die pq-Formel verwendest du bei quadratischen Gleichungen, nicht bei linearen. Du hättest sie in diesem Fall bei den Extremstellen verwenden können, indem du die 1. Ableitung = 0 setzt. Dann hast du auch p und q.

Answer 3

B scheint der Wendepunkt sein.

Wendestelle bestimmen:

f ''(x) = 0

xW= ...

xW in die 1. Ableitung einsetzen

tan a = f '(xW)

Wie kommst du auf 2 Wendestellen?

6,78x- 5,18 = 0

x= 0,764

f '(0,764) = ....