Bestimmen Sie die Größe des Winkels zwischen den Vektoren a und b

Question

Bestimmen Sie die Größe des Winkels zwischen den Vektoren \(\vec a\) und \(\vec b\) .
a)
\(\vec a = \begin{pmatrix} 3\\1 \end{pmatrix}\),

\(\vec b = \begin{pmatrix} 3\\-3 \end{pmatrix}\)

Answer 1

Hi,

Es ist

$$\cos(\alpha) = \frac{\vec a\cdot \vec b}{|\vec a|\cdot |\vec b|}$$

Grüße

Answer 2

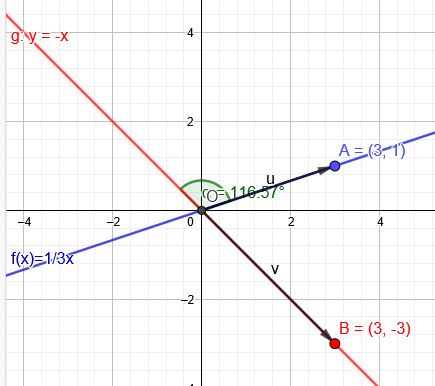
Steigung der Ursprungsgeraden durch \(A(3 |1)\): \(m_1=\frac{1}{3} \)

Steigung der Ursprungsgeraden durch \(B(3|-3)\): \(m_2=-1 \)

Winkel zwischen Geraden:

 \(\tan(α)=|\frac{m_2-m_1}{1+m_1 \cdot m_2}|\)

\(\tan(α)=|\frac{-1-\frac{1}{3} }{1+\frac{1}{3} \cdot (-1)}|=|-2|=2\)

\( \tan^{-1}(2)= α=63,43° \)