Aufgabe:
Steigung in Richtung x1 und x2 berechnen.
Problem/Ansatz:
Ich bekomme die Steigung in Richtung x2 nicht raus. Mein Ansatz ist doch richtig, aber laut Musterlösung ist es 10. Ich komme allerdings auf 24. Kann mir jemand helfen?
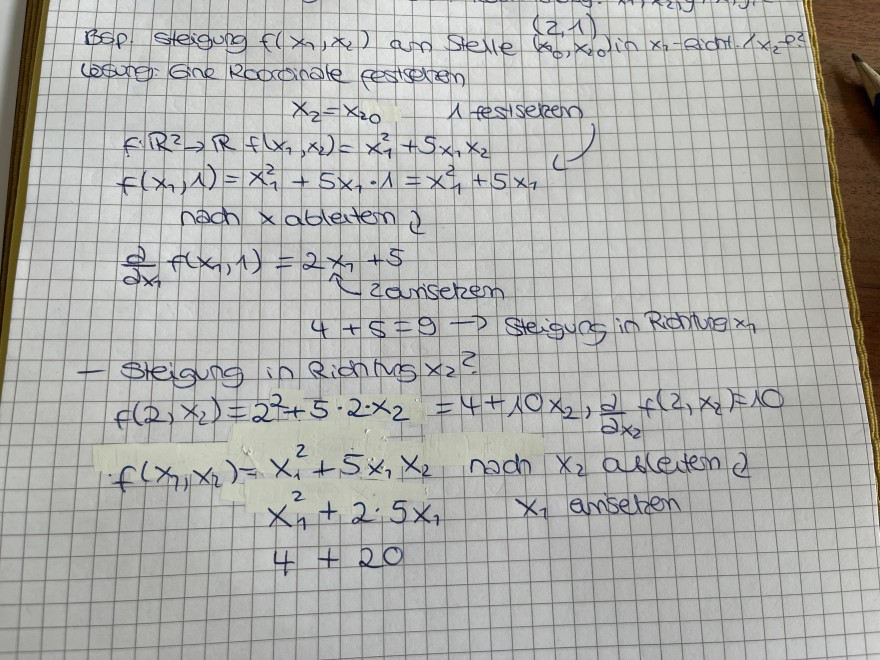
Text erkannt:
losung: Gine Roorcinate pestsetion
\( \begin{array}{l} x_{2}=x_{20} \quad 1 \text { festseizen } \\ f \cdot \mathbb{R}^{2} \rightarrow \mathbb{R} f\left(x_{1}, x_{2}\right)=x_{1}^{2}+5 x_{1} x_{2} \\ f\left(x_{1}, 1\right)=x_{1}^{2}+5 x_{1} \cdot 1=x_{1}^{2}+5 x_{1} \end{array} \)
nach \( x \) ableiten ?
\( \frac{\partial}{\partial x_{1}} f\left(x_{1}, 1\right)=2 x_{1}+5 \)
zarisetzen
\( 4+5=9 \rightarrow \) Steigung in Ridhtung \( x_{1} \)
- Steigung in Rionlus \( x_{2} \) ?
\( f\left(2, x_{2}\right)=2^{2}+5 \cdot 2 \cdot x_{2}=4+10 x_{2}, \frac{d}{\partial x_{2}} f\left(2, x_{2}\right)=10 \)
\( f\left(x_{1}, x_{2}\right)=x_{1}^{2}+5 x_{1} x_{2} \) nadn \( x_{2} \) ableten \&
\( x_{1}^{2}+2 \cdot 5 x_{1} \quad x_{1} \) anseten
\( 4+20 \)
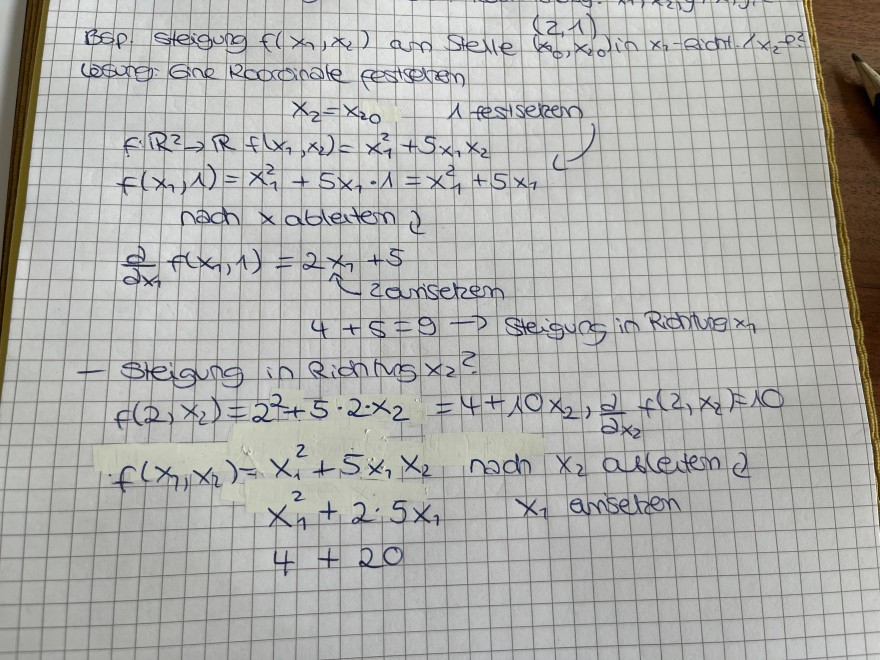
Text erkannt:
losung: Gine Roorcinate pestsetion
\( \begin{array}{l} x_{2}=x_{20} \quad 1 \text { festseizen } \\ f \cdot \mathbb{R}^{2} \rightarrow \mathbb{R} f\left(x_{1}, x_{2}\right)=x_{1}^{2}+5 x_{1} x_{2} \\ f\left(x_{1}, 1\right)=x_{1}^{2}+5 x_{1} \cdot 1=x_{1}^{2}+5 x_{1} \end{array} \)
nach \( x \) ableiten ?
\( \frac{\partial}{\partial x_{1}} f\left(x_{1}, 1\right)=2 x_{1}+5 \)
zarisetzen
\( 4+5=9 \rightarrow \) Steigung in Ridhtung \( x_{1} \)
- Steigung in Rionlus \( x_{2} \) ?
\( f\left(2, x_{2}\right)=2^{2}+5 \cdot 2 \cdot x_{2}=4+10 x_{2}, \frac{d}{\partial x_{2}} f\left(2, x_{2}\right)=10 \)
\( f\left(x_{1}, x_{2}\right)=x_{1}^{2}+5 x_{1} x_{2} \) nadn \( x_{2} \) ableten \&
\( x_{1}^{2}+2 \cdot 5 x_{1} \quad x_{1} \) anseten
\( 4+20 \)