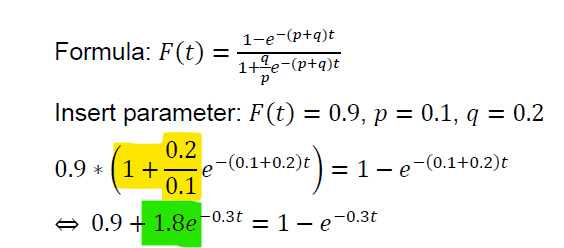
Text erkannt:
Formula: \( F(t)=\frac{1-e^{-(p+q) t}}{1+\frac{q}{p} e^{-(p+q) t}} \)
Insert parameter: \( F(t)=0.9, p=0.1, q=0.2 \)
\( \begin{array}{l} 0.9 *\left(1+\frac{0.2}{0.1} e^{-(0.1+0.2) t}\right)=1-e^{-(0.1+0.2) t} \\ \Leftrightarrow 0.9+1.8 e^{-0.3 t}=1-e^{-0.3 t} \end{array} \)
Wie komme ich vom dem gelb markierten Ausdruck zu dem grünen?
Und weshalb löst sich die Klammer auf? Mit der 0.9 wurde ja anscheinend nicht ausmultipliziert...