Du hast einen Vorzeichenfehler und hast noch einen unnötigen Faktor 2 in deinem Ausdruck für \(y'\).
Die Ausgangsgleichung ist
\(\boxed{(x-3)^2+(y-5)^2=36\quad (1)}\)
Implizite Differentiation ergibt
\(2(x-3) + 2(y-5)y' = 0 \Leftrightarrow (x-3) + (y-5)y' = 0\)
\(\stackrel{y-5 \neq 0}{\Leftrightarrow} \boxed{y' = -\frac{x-3}{y-5} \quad (2)}\)
Waagerechte Tangente:
\(\bm{y'=0} \Leftrightarrow x=3\) und \(y(3)\neq 5\)
Einsetzen von \(x=3\) in (1) ergibt
\(y=-1\) und \(y=11\).
\(\Rightarrow\) waagerechte Tangente in \((3|-1)\) und \((3|11)\).
Senkrechte Tangente:
\(\bm{|y'|=\infty} \Leftrightarrow y=5\) und \(x(5)\neq 3\)
Einsetzen von \(y=5\) in (1) ergibt
\(x=-3\) und \(x=9\).
\(\Rightarrow\) senkrechte Tangente in \((-3|5)\) und \((9|5)\).
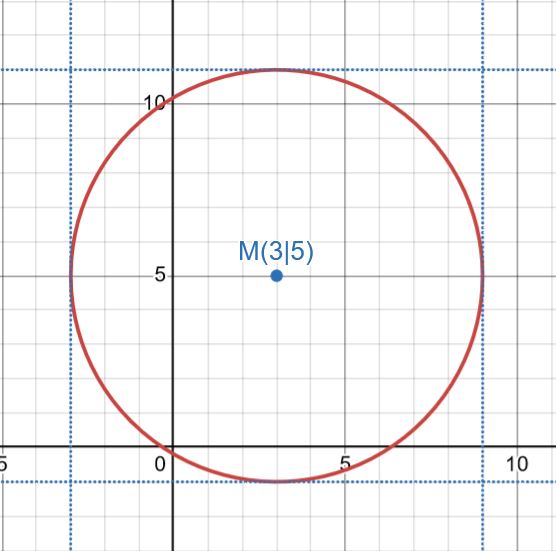
Das Ergebnis ist nicht überraschend, denn Gleichung (1) ist eine Kreisgleichung: