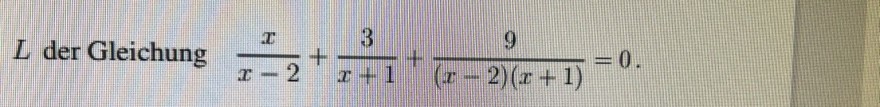
Text erkannt:
\( L \) der Gleichung \( \frac{x}{x-2}+\frac{3}{x+1}+\frac{9}{(x-2)(x+1)}=0 \).

Text erkannt:
\( \begin{array}{l}\frac{x}{x-2}+\frac{3}{x+1}+\frac{9}{(x-2)(x+1)}=0 \quad 0=\mathbb{R} \backslash 2,-1, \\ \frac{x}{x-2}+\frac{3}{x+1}+\frac{9}{x^{2}-x-2}=0 \quad \cdot x^{2}-x-2 \\ \frac{x}{x-2}+\frac{3}{x+1}+9 \\ \frac{x}{x-2} \cdot \frac{x^{2}-x-2}{1}+\frac{3}{x+1} \cdot \frac{x^{2}-x-2}{1}+9=0 \\ \frac{x \cdot x^{2}-x-2}{x-2}+\frac{3 \cdot x^{2}-x-2}{x+1}+9=0\end{array} \)
Hallo (potentielle) Lebensretter,
ich soll die Lösungsmenge zur oberen Gleichung finden. Leider hab ich sehr große Lücken, die Schule liegt lange Zeit zurück.
Auf dem Blatt könnt ihr sehen, was ich mir überlegt hab. Geht das überhaupt in die richtige Richtung ? Kann mir jemand helfen, wie ich weiter machen könnte ? Ich hätte vermutet, dass ich nun die restlichen Brüche irgendwie durch faktorisieren und kürzen weg bekommen muss. Oder muss ich irgendwie die Form für die abc-Formel hin bekommen ?
Danke im Voraus!
