Text erkannt:
Eine Fabrik produziert Kugellager. Diese Kugellager sollen alle den gleichen Umfang von \( 10 \mathrm{~cm} \) aufweisen. Bei der Weiterverarbeitung wurde jedoch festgestellt, dass der Umfang mancher Kugellager vom eingestellten Wert \( \mu_{0}=10 \mathrm{~cm} \) abweicht. Daher wurde eine Stichprobe genommen und von 21 Kugellagern der Umfang nachgemessen. Diese Stichprobe lieferte folgende Ergebnisse:
\begin{tabular}{|c|c|c|}
\hline Anzahl & Mittelwert & Stichprobenvarianz \\
\hline 21 & 10.31 & 0.38 \\
\hline
\end{tabular}
Versuchen Sie (statistisch) nachzuweisen, dass der Umfang der Kugellager im Mittel dem Sollwert nicht entspricht. Verwenden Sie ein Signifikanzniveau von \( 5 \% \). Beantworten Sie folgende Fragen:
a.1. Das dazugehörige Hypothesenpaar lautet: \( H_{0}: \mu=10 \quad H_{1}: \mu \neq 10 \)
a.2. Das dazugehörige Hypothesenpaar lautet: \( H_{0}: \mu \neq 10 \quad H_{1}: \mu=10 \)
a.3. Das dazugehörige Hypothesenpaar lautet: \( H_{0}: \mu \geq 10 \quad H_{1}: \mu<10 \)
a.4. Das dazugehörige Hypothesenpaar lautet: \( H_{0}: \mu>10 \quad H_{1}: \mu \leq 10 \)
b. Wie lautet der Absolutbetrag der Teststatistik? 2.3
c. Wie lautet der entsprechende kritische Wert? -1.72
d.1. \( H_{0} \) kann nicht abgelehnt werden.
d.2. \( H_{0} \) kann abgelehnt werden.

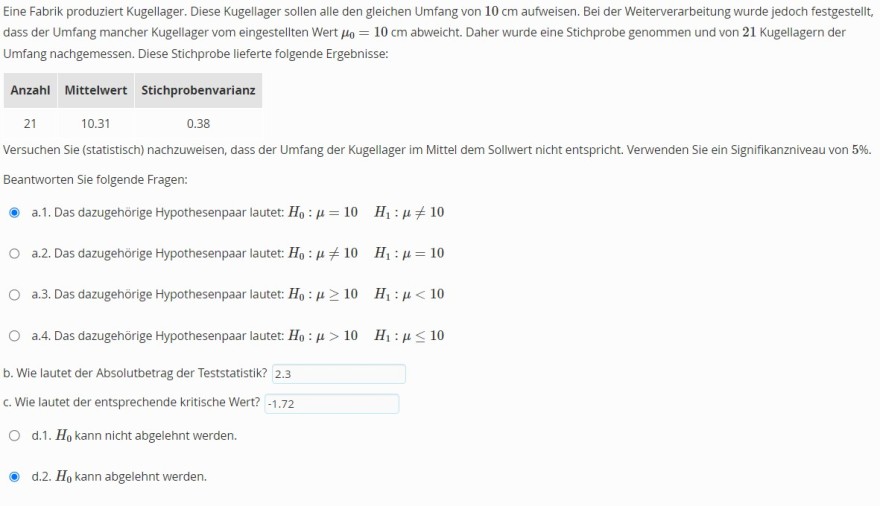
Text erkannt:
\( >q t(0.05,20) \)
[1] -1.724718
\( >(10.31-10) / \operatorname{sqrt}(0.38) * \operatorname{sqrt}(21) \)
[1] 2.304515
Habe den unteren Code in R eingegeben, eine meiner Antworten ist jedoch falsch. Welche könnte es sein? Danke!