Begründen Sie, dass es sich bei dem abgebildeten Graphen nicht um den Graphen von f handeln kann.

Question

Text erkannt:

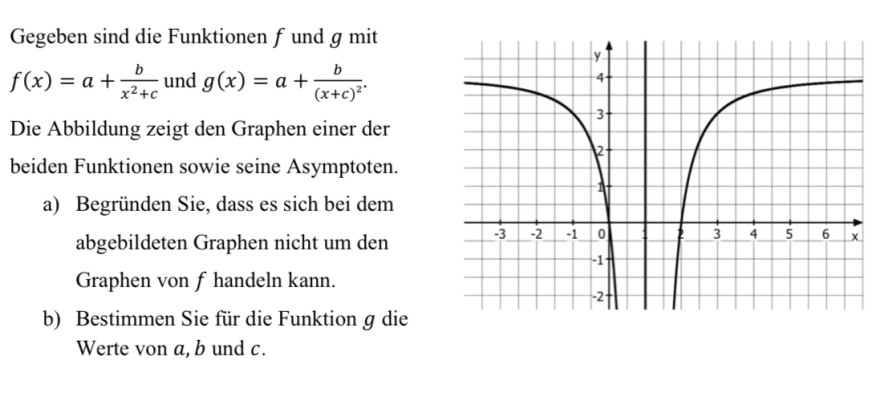
Gegeben sind die Funktionen \( f \) und \( g \) mit \( f(x)=a+\frac{b}{x^{2}+c} \) und \( g(x)=a+\frac{b}{(x+c)^{2}} \). Die Abbildung zeigt den Graphen einer der beiden Funktionen sowie seine Asymptoten.
a) Begründen Sie, dass es sich bei dem abgebildeten Graphen nicht um den Graphen von \( f \) handeln kann.
b) Bestimmen Sie für die Funktion \( g \) die Werte von \( a, b \) und \( c \).

Bitte keine Lösung sondern nur Unterstützung, vielen Dank

Answer 1

f hat keine Polstelle.

Von g hast du Nullstellen, Polstelle und (nicht abgebildet) eine waagerechte Asymptote, die vermutlich y=4 ist.

Comments

Richtig wäre : f hat eine gerade Anzahl von Polstellen ≠ 0

---

Hat f nicht genau eine Polstelle für c = 0 und genau zwei Polstellen für c < 0?

Answer 2

a)

Was kannst du bezüglich der Symmetrie von f aussagen?

b)

Verwende die Asymptote um a zu bestimmen.

Verwende die Symmetrie um c zu bestimmen.

Verwende die Nullstellen um b zu bestimmen.