Bestimmen Sie die Fläche zwischen zwei Graphen

Question

Aufgabe:

Gegeben seien die Funktionen
f（x） =-x⁴ +8,5x² +4.5 und g（x）= -2,75x² +24,75
Der Graph von f ist unten dargestellt.

Problem/Ansatz:

a) Bestimmen Sie die Schnittpunkte des Graphen von g mit den Koordinatenachsen sowie mit dem Graphen von fund zeichnen sie ihn im selben Koordinatensystem.
b) Bestimmen Sie den Inhalt der Fläche, die von den Graphen von f und g vollständig eingeschlossen wird.

Ich habe schon a) gemacht und rausgefunden das Schnittpunkte 3, -3 und 1.5, -1.5 sind. aber beim b) komme ich nicht klar

Würde mich sehr bedanken wenn jemand es mir erklären könnte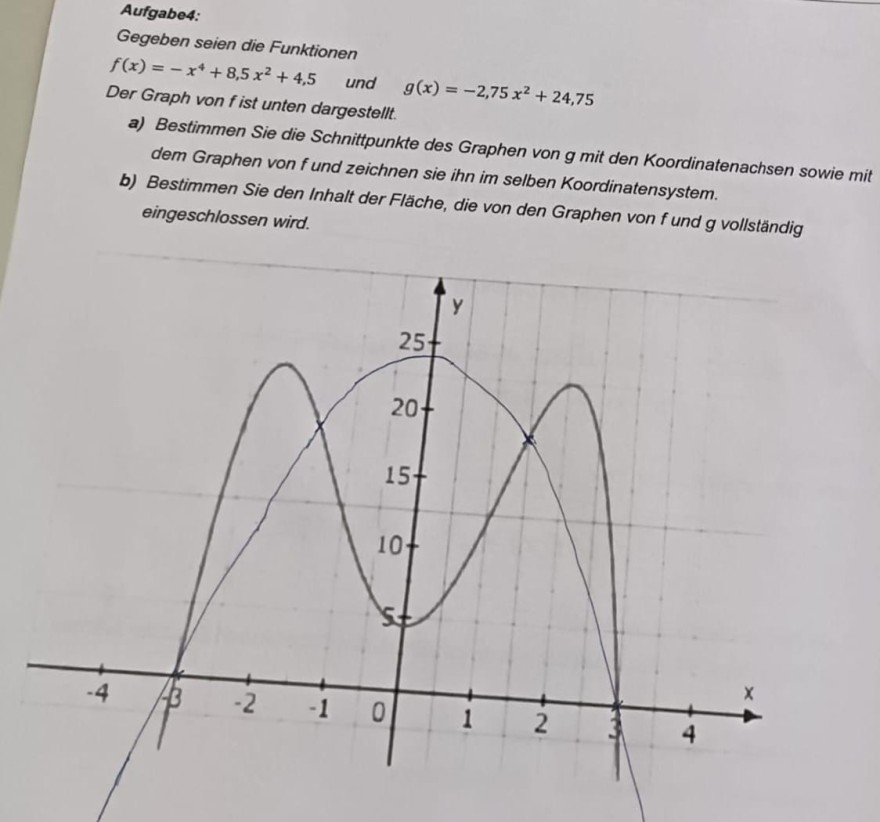

Text erkannt:

Aufgabe4:
Gegeben seien die Funktionen
$\begin{array}{l} f(x)=-x^{4}+8,5 x^{2}+4,5 \text { und } g(x)=-2,75 x^{2}+24,75 \\ \text { Der Graph von } f \text { ist unten dargestellt } \end{array}$

Der Graph von $f$ ist unten dargestellt.
a) Bestimmen Sie die Schnittpunkte des Graphen von g mit den Koordinatenachsen sowie mit dem Graphen von fund zeichnen sie ihn im selben Koordinatensystem.
b) Bestimmen Sie den Inhalt der Fläche, die von den Graphen von $f$ und $g$ vollständig eingeschlossen wird.

Comments

Markiere die relevanten Flächen und nutze die Symmetrie aus.

Betrachte nur [0;3]

---

Also muss ich auch von 1.5 bis 3 ausrechnen?
Bin gerade komplett verwirrt; habe versucht skitze zu machen, dachte ich kann nur von f(x) von 0 bis 1.5 ausrechnen und dann differenz zwischen f und g, 1.5 bis 3

oder nur von 0 bis 3 und dann mal 2?
Danke nochmal

Answer 1

b) Bestimmen Sie den Inhalt der Fläche, die von den Graphen von f und g vollständig eingeschlossen wird.

$f（x)=-x^4 +8,5x^2 +4,5$ und $g(x)=-2,75 x^{2}+24,75$

Differenzfunktion:

$d(x)=g(x)-f（x)$

$d(x)=-2,75 x^{2}+24,75-(-x^4 +8,5x^2 +4,5)$

$A=2\cdot\int\limits_{0}^{1,5}d(x)dx$   wegen Symmetrie zur y-Achse.

Diese Lösung ist noch nicht vollständig. Ich habe den Bereich von 1,5 bis 3 vergessen.

Comments

Also muss ich auch von 1.5 bis 3 ausrechnen?

Bin gerade komplett verwirrt; habe versucht skitze zu machen, dachte ich kann nur von f(x) von 0 bis 1.5 ausrechnen und dann differenz zwischen f und g, 1.5 bis 3

Danke nochmal

---

Die Fläche, die vollständig eingeschlossen wird. Male sie mit Textmarker in Neongelb an. Damit klärt sich dann hoffentlich deine Frage.

---

Also erstmal von 0 bis 1.5 und dann 1.5 bis 3 und dann alles mal 2 wenn ich es richtig verstanden habe

---

So ist es. Du kannst von dem zweiten Integral entweder den Betrag nehmen oder die Funktionen vertauschen, da sie dort ja "wechseln".

---

Achso habe es endlich verstanden, danke nochmal

Answer 2

Nur zur Kontrolle:

$\int \limits_{-3}^{3}\left|\left(-x^{4}+8.5 \cdot x^{2}+4.5\right)-\left(-2.75 \cdot x^{2}+24.75\right)\right| d x=\frac{243}{4} = 60.75$

Comments

Also muss ich auch von 1.5 bis 3 ausrechnen?
Bin gerade komplett verwirrt; habe versucht skitze zu machen, dachte ich kann nur von f(x) von 0 bis 1.5 ausrechnen und dann differenz zwischen f und g, 1.5 bis 3
Danke nochmal

---

Ja du berechnest 2 Integrale. Einmal von 0 bis 1.5 und einmal von 1.5 bis 3. Du erhältst zwei Werte, deren Beträge du addierst. Die Summe multiplizierst du am Ende noch mal 2. Wenn du das machst solltest du hoffentlich auf meine Kontroll-Lösung kommen.

---

Nur eine Frage noch zwischen 0 bis 1.5 rechen ich auch differenz zwischen beide funktionen oder reicht nur f(x)

---

Nur eine Frage noch zwischen 0 bis 1.5 rechen ich auch differenz zwischen beide funktionen oder reicht nur f(x)

Richtig auch dort nimmt du die Differenz, denn auch dort geht es um die Fläche zwischen g und f und nicht nur um die Fläche zwischen einer Funktion und der x-Achse.