Hallo Mathelounge community,
Ich habe wieder mal einen Ansatz jedoch keine Ahnung ob das richtig wäre, und wollte fragen ob mir jemand vlt. helfen könnte und darüber schauen könnte.
Danke im voraus!
Die Aufgabe:
Fur eine relle Zahl α und eine naturliche Zahl k werde der allgemeine Binomialkoeffizient wie folgt definiert
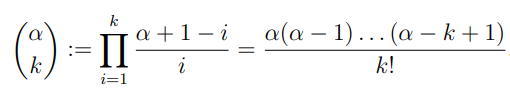
Mit a über 0 = 1
a)
Beweisen Sie fur alle ¨ α ∈ R und alle k ∈ N, dass gilt:
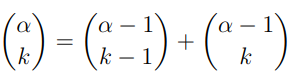
b)
Man beweise fur alle reellen Zahlen x, y und fur alle n ∈ N, dass gilt .
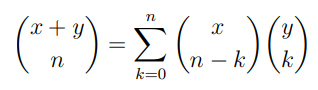
Mein Ansatz:
a)
Zu zeigen: gillt für alle α∈R und k∈N
$$ \binom{\alpha}{k} = \frac{\alpha(\alpha - 1)...(\alpha - k + 1)}{k!} $$
Um dies zu beweisen, können wir die Definition des Binomialkoeffizienten verwenden: Beginnen wir mit der rechten Seite der Gleichung:
$$ \binom{\alpha - 1}{k - 1} + \binom{\alpha - 1}{k} = \frac{(\alpha - 1)!}{(k - 1)!(\alpha - k)!} + \frac{(\alpha - 1)!}{k!(\alpha - k - 1)!} $$
Anschliesent führt man die Terme zusammen
$$ = \frac{\alpha(\alpha - 1)!}{k!(\alpha - k)!} = \binom{\alpha}{k} $$
Das beweist die Behauptung für (a)
(b) Der binomische Lehrsatz besagt, dass
$$ (x + y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^k $$
weiter kam ich nicht, ich habe es auch anshcließend über induktion versucht aber nicht geschafft und brauche hier ammeisten hilfe.
$$ \binom{x + y}{n} = \sum_{k=0}^{n} \binom{x}{n - k} \binom{y}{k} $$