Habt ihr eine Idee, wie man die Mengen zuordnen könnte? Meine Vermutung ist, dass A zu 4 gehören muss.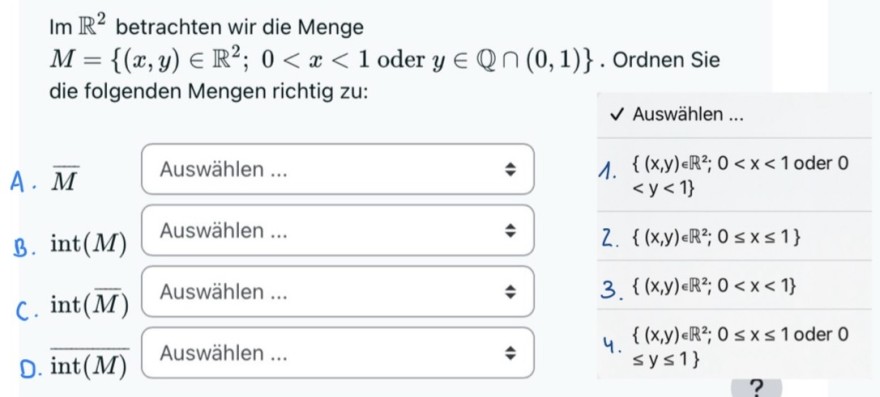
Text erkannt:
Im \( \mathbb{R}^{2} \) betrachten wir die Menge
\( M=\left\{(x, y) \in \mathbb{R}^{2} ; 0<x<1\right. \) oder \( \left.y \in \mathbb{Q} \cap(0,1)\right\} \). Ordnen Sie die folgenden Mengen richtig zu:
A. \( \bar{M} \)
Auswählen ...
\( \checkmark \) Auswählen ...
1. \( \left\{(x, y) \in \mathbb{R}^{2} ; 0<x<1\right. \) oder 0 \( <y<1\} \)
B. \( \operatorname{int}(M) \)
Auswählen ...
2. \( \left\{(x, y) \in \mathbb{R}^{2} ; 0 \leq x \leq 1\right\} \)
\( \operatorname{int}(\bar{M}) \)
Auswählen ...
3. \( \left\{(x, y) \in \mathbb{R}^{2} ; 0<x<1\right\} \)
4. \( \left\{(\mathrm{x}, \mathrm{y}) \in \mathbb{R}^{2} ; 0 \leq \mathrm{x} \leq 1\right. \) oder 0
\( \overline{\operatorname{int}(M)} \)
Auswählen ...
\( \leq y \leq 1\} \)