Stelle einen Term für den Umfang und Flächeninhalt auf

Question

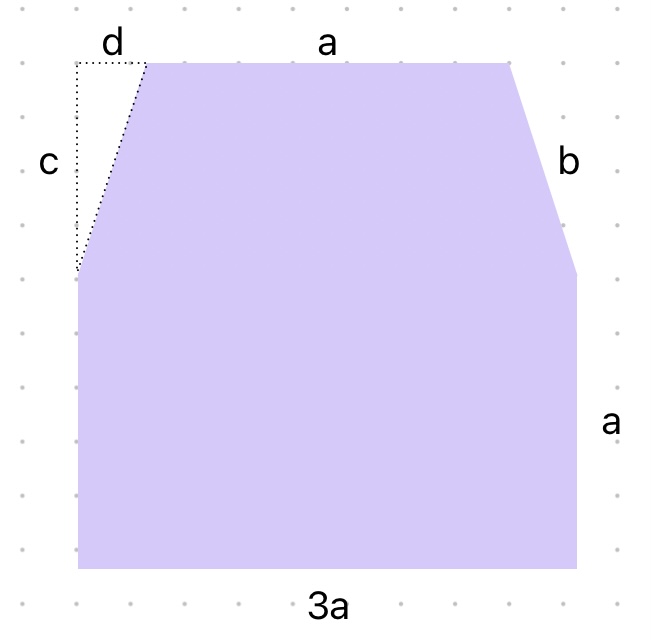
Aufgabe:

Guten Abend zusammen, ich stehe vor der Herausforderung, einen Term für folgendes zu formulieren:

a) den Umfang und

b) den Flächeninhalt einer gegebenen Fläche.

Problem/Ansatz: Mit dem Umfang habe ich keine Schwierigkeiten. Allerdings bereitet mir das Aufstellen des Terms für den Flächeninhalt Kopfzerbrechen. Es gibt zwei Ansätze, die ich verfolgt habe:

1. Möglichkeit - Subtraktion von Teilflächen: Ich habe zunächst den Flächeninhalt eines Rechtecks mit den Maßen (3a*(a+c)) berechnet. Danach habe ich die Flächeninhalte der Dreiecke links und rechts subtrahiert (1/2*c*d). So kam ich auf den Term: 3a²+3ac-cd

2. Möglichkeit - Zerlegung in kleinere Flächen: Ich habe die Fläche in ein gleichschenkliges Trapez (1/2*(3a+a)*c) und ein Rechteck (3a*a) zerlegt. Anschließend die beiden Flächeninhalte addiert. Daraus resultierte der Term: 3a²+2ac

Frage: Warum erhalte ich unterschiedliche Terme? Wenn ich die Variablen mit den Werten (a=7cm), (b=5cm), (c=2cm) und (d=4cm) einsetze, ergeben sich auch unterschiedliche Resultate.
Kann mir jemand erklären, wo mein Fehler liegt?
Vielen Dank im Voraus!

Liebe Grüße

Comments

Naja, da stimmt etwas nicht mit der Skizze, soweit ich das verstehe. Der untere Rand ist 3a. Der obere a+2d. Dann sollte d=a sein, oder?

Answer 1

Warum erhalte ich unterschiedliche Terme?

Du hast in dem Term 3a²+3ac-cd den Zusammenhang d = a nicht verwendet.

(a=7cm), (b=5cm), (c=2cm) und (d=4cm)

Da ist d ≠ a. Die Maße passen deshalb nicht auf die gegebene Figur.

Comments

Tatsächlich! Der korrekte Term ist also

3a² +2ac

Vielen Dank!

---

Der Term 3a²+3ac-cd ist ebenso korrekt.

---

Aber nur wenn d=a ist, richtig? Also könnte man es auch als 3a²+3ac-ca darstellen? Und das wäre dann 3a² +2ac