Hast du schon beim Schrägbild Probleme? Aufgrund des Schrägbildes solltest du bereits eine Vermutung haben, welcher Punkt sich auf welcher Geraden befinden könnte. Das ist dann nur noch rechnerisch zu prüfen.
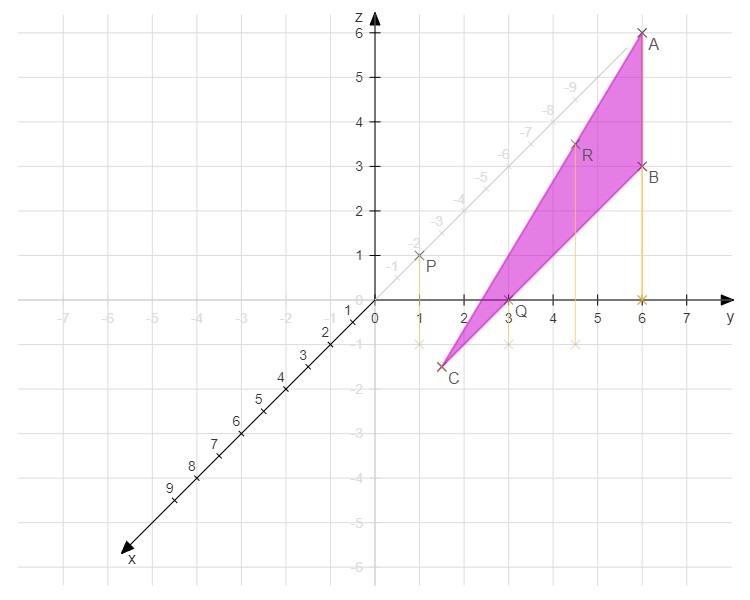
Liegt Q auf der Gerade durch B und C ?
[0, 6, 3] + r * ([3, 3, 0] - [0, 6, 3]) = [2, 4, 1] --> r = 2/3
Q befindet sich auf der Geraden.
Liegt R auf der Gerade durch A und C
[0, 6, 6] + r * ([3, 3, 0] - [0, 6, 6]) = [2, 5.5, 4.5] → keine Lösung
R befindet sich nicht auf der Geraden.