Zur Aufgabe b)
Wir haben zwei rechtwinklige Dreiecke mit c = 7cm, γ = 90° und β = 43°/2 = 21,5°:
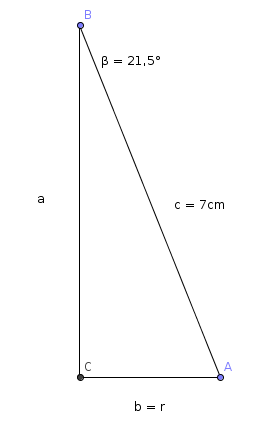
Aus dem Sinus-Satz folgt
c/sin(γ) = b/sin(β)
7cm/1 = b/sin(21,5)
b = 7cm * sin(21,5) ≈ 2,5655085871cm
Umfang der Grundfläche ist also 2 * π * r =
2 * π * 7cm * sin(21,5) ≈ 16,12cm
Ohne Garantie :-)
zur Aufgabe c)
Pfadwahrscheinlichkeit x = 1 - 3/12 = 9/12, denn die beiden "Äste" müssen sich ja zu 1 ergänzen.
In der Urne sind also insgesamt zu Beginn 12 Kugeln, und zwar 3 weiße und 9 schwarze.
Wenn also im 1. Zug eine schwarze Kugel gezogen wird, sind von den verbliebenen 11 Kugeln noch 8 schwarze in der Urne, so dass sich für y ergibt: y = 8/11