Berechnen Sie mit der Regel von L'Hospital die folgenden Grenzwerte.

Question

Aufgabe:

Text erkannt:

Berechnen Sie mit der Regel von L'Hospital die folgenden Grenzwerte. (Betrachten Sie die entstehenden Terme und klammern Sie ggf. aus.)
a)
\( \lim \limits_{x \rightarrow \infty \rightarrow \infty} \frac{\ln \left(6+e^{x}\right)}{\sqrt{5+5 x^{2}}}=\square \sqrt{5+5 x^{2}}=\frac{\ln \left(6+e^{x}\right)}{\sqrt{5+5 \infty}} \)

Problem/Ansatz:

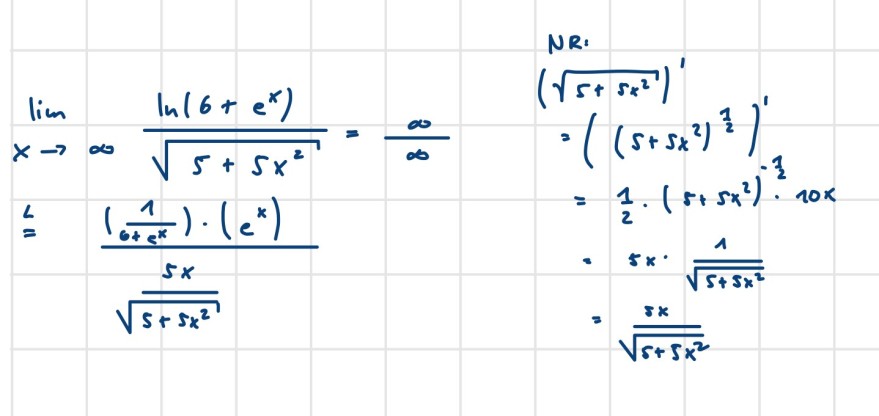
Meine Frage ist jetzt: Wie mache ich weiter? Was kann ich umformen? Kann mir da jemand bitte helfen.

Answer 1

Entscheide Dich beim Aufschreiben für "mit lines" oder "ohne limes" - gemischt geht nicht.

Soweit richtig. Nun natürlich erstmal Doppelbrüche auflösen. Dann betrachte die Faktoren getrennt: \(\lim \frac{e^x}{6+e^x}\) ausrechnen und \(\lim\frac{\sqrt{5+5x^2}}{5x}\) ausrechnen. Für letzteres die \(5x\) unter die Wurzel bringen. Du solltest am Ende auf \(\frac1{\sqrt{5}}\) kommen.

Answer 2

Verwende:

e^x/(e^x+1) = (e^x+1-1)/(e^x+1) = 1- 1/(e^x+1)  -> 1 für x -> oo

Klammere in Nenner x aus der Wurzel aus:

5x/(x*√(5/x^2+5)

Kürze dann mit x: