Intervalle berechnen in denen f(x) = sin x positiv ist.

Question

Aufgabe:

\( f(x)=\sin x, \quad D_{f}=[0,2 \Pi] \)

Man berechne die Intervalle, in denen:

a) f(x) positiv/negativ

b) f(x) monoton steigend/fallend

c) f(x) links-/rechtsgekrümmt

ist.

Außerdem wie kann ich die oben gegebene Funktionen zeichnen

Answer 1

Für diese Aufgabe musst du schon wissen, wie die Sinusfunktion aussieht.

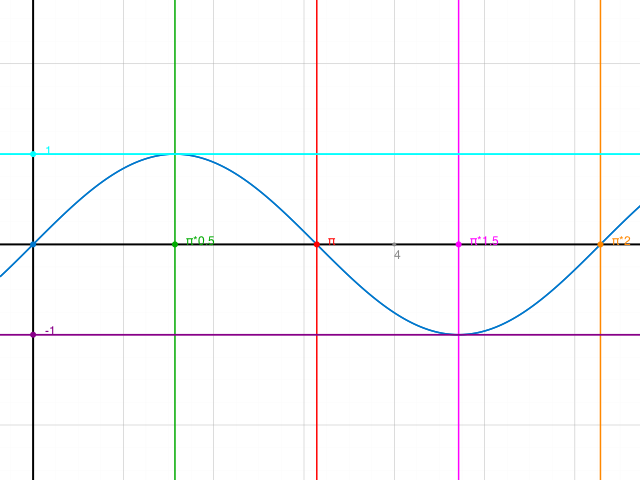
Nun kannst du die Antworten zu a),b) und c) ablesen:

 

a) f (x) positiv/negativ 

in (0,π) ist f(x) positiv

in (π,2π) ist f(x) negativ

b)f (x) monoton steigend/fallend

in [0,π/2] und [3π/2, 2π] ist f(x) monoton steigend

in [π/2, 3π/2] ist f(x) monoton fallend

c)f (x) links-/rechtsgekrümmt 

in (0,π) ist f rechtsgekrümmt
in (π,2π) ist f linksgekrümmt

Einführendes Video zum Sinus und Bezug zum Einheitskreis vgl: https://www.matheretter.de/wiki/einheitskreis